辽宁省丹东十七中2017年中考数学二模试卷
试卷更新日期:2017-11-09 类型:中考模拟
一、选择题
-
1. ﹣ 的绝对值是( )A、 B、﹣ C、 D、﹣2. 下列各式中,计算正确的是( )
A、2x+3y=5xy B、x6÷x2=x3 C、x2•x3=x5 D、(﹣x3)3=x63. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,在数轴上表示不等式组 的解集,其中正确的是( )A、
4. 如图,在数轴上表示不等式组 的解集,其中正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、16个 B、15个 C、13个 D、12个6. 如图是4块小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小方块的个数,其主视图是( )
5. 在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、16个 B、15个 C、13个 D、12个6. 如图是4块小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小方块的个数,其主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如果三角形的两边长分别是方程x2﹣8x+15=0的两个根,那么连接这个三角形三边的中点,得到的三角形的周长可能是( )
7. 如果三角形的两边长分别是方程x2﹣8x+15=0的两个根,那么连接这个三角形三边的中点,得到的三角形的周长可能是( )
A、5.5 B、5 C、4.5 D、48. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: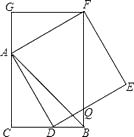
①AC=FG; ②S△FAB:S四边形CBFG=1:2;
③∠ABC=∠ABF; ④AD2=FQ•AC,
其中正确的结论的个数是( )
A、1 B、2 C、3 D、4二、二.填空题
-
9. 在综合实践课上.五名同学做的作品的数量(单位:件)分别是:5,7,3,6,4,则这组数据的中位数是件.
10. 函数y= 有意义,则自变量x的取值范围是 .11. 在平面直角坐标系中,把抛物线y= +1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是 .12. 如图,点P是正比例函数y=x与反比例函数y= 在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为2,则k的值是 . 13. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 .
13. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 . 14. 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=3,则DF的长为 .
14. 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=3,则DF的长为 .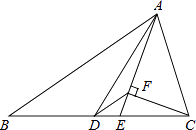 15. 如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1 , 以A1B.BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2 , 以A2B1 . B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
15. 如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1 , 以A1B.BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2 , 以A2B1 . B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
三、解答题
-
16. 先化简,再求值:(a﹣ )÷ ,其中,a=( )﹣1+tan45°.17. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).

①若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),画出图形并直接写出顶点A1 , B1的坐标;
②将△ABC绕着点O按逆时针方向旋转90°得到A3B3C3 , 请直接写出点A所经过的路径长.
四、解答题
-
18. 为了了解青少年形体情况,现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对测评数据作了适当处理(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
 (1)、请问这次被抽查形体测评的学生一共是多少人?(2)、请将两幅统计图补充完整.(3)、如果全市有5万名初中生,那么全市初中生中,坐姿和站姿不良的学生有多少人?19. 某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:(1)、该顾客至少可得元购物券,至多可得元购物券;(2)、请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
(1)、请问这次被抽查形体测评的学生一共是多少人?(2)、请将两幅统计图补充完整.(3)、如果全市有5万名初中生,那么全市初中生中,坐姿和站姿不良的学生有多少人?19. 某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:(1)、该顾客至少可得元购物券,至多可得元购物券;(2)、请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.五、解答题
-
20. 如图,AB是⊙O的直径,点D是 上一点,且∠BDE=∠CBE,BD与AE交于点F.
 (1)、求证:BC是⊙O的切线;(2)、若BD平分∠ABE,求证:DE2=DF•DB;(3)、在(2)的条件下,延长ED、BA交于点P,若PA=AO,DE=2,求PD的长.21. “母亲节”前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着又用5000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价是多少元?
(1)、求证:BC是⊙O的切线;(2)、若BD平分∠ABE,求证:DE2=DF•DB;(3)、在(2)的条件下,延长ED、BA交于点P,若PA=AO,DE=2,求PD的长.21. “母亲节”前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着又用5000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价是多少元?
六、解答题
-
22. 如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数, ≈1.7, ≈1.4 )
 23. 为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.(1)、李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)、设李明获得的利润为W(元),当销售单价为多少元时,每月可获得最大利润?(3)、物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为 元(直接写出结果)
23. 为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.(1)、李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)、设李明获得的利润为W(元),当销售单价为多少元时,每月可获得最大利润?(3)、物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为 元(直接写出结果)
七、解答题
-
24. 如图,四边形ABCD是正方形,E是边AB上一点,连接DE,将直线DE绕点D逆时针旋转90°,交BC的延长线于点F.(1)、如图1,求证:DE=DF;
 (2)、如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E为AP中点;
(2)、如图2,连接EF,若D关于直线EF的对称点为H,连接CH,过点H作PH⊥CH交AB于点P,求证:E为AP中点; (3)、如图3,在(2)的条件下,连接AC交EF于点G,连接BG,BH,若BG= ,AB=3,求线段BH的长
(3)、如图3,在(2)的条件下,连接AC交EF于点G,连接BG,BH,若BG= ,AB=3,求线段BH的长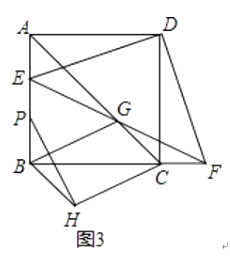
八、解答题
-
25. 如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点.交y轴与C点,已知抛物线的对称轴为x=1,B(3,0),C(0,﹣3)
 (1)、求这条抛物线所对应的函数关系式;(2)、在抛物线的对称轴上是否存在一点P,使点P到A,C两点的距离之和最小?若存在,求出点P的坐标;若不存在,请说明理由
(1)、求这条抛物线所对应的函数关系式;(2)、在抛物线的对称轴上是否存在一点P,使点P到A,C两点的距离之和最小?若存在,求出点P的坐标;若不存在,请说明理由
(3)、在抛物线上是否存在一点M,使∠MAB=45°?若存在,求出点M的坐标;若不存在,请说明理由(4)、若点G在直线BC上,点H在抛物线上,是否存在这样的点G,点H,使得以G,H,O,C为顶点的四边形是平行四边形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
-