河南省鹤壁市2017年中考数学模拟试卷
试卷更新日期:2017-11-09 类型:中考模拟
一、选择题
-
1. 实数2017的倒数的相反数是( )A、 B、﹣ C、﹣2017 D、20172. 中国科学家屠呦呦获得了诺贝尔生理学或医学奖,她研发的抗疟新药每年能为近120万婴幼儿免除疟疾的危害.其中120万用科学记数法表示为( )A、12×103 B、1.2×104 C、1.2×106 D、1.2×1083. 下列几何体中,主视图是等腰三角形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、(﹣x3)4=x12 B、x8÷x4=x2 C、x2+x4=x6 D、(﹣x)﹣1=5. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
4. 下列运算正确的是( )A、(﹣x3)4=x12 B、x8÷x4=x2 C、x2+x4=x6 D、(﹣x)﹣1=5. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( ) A、边边边 B、边角边 C、角边角 D、角角边6. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为( )
A、边边边 B、边角边 C、角边角 D、角角边6. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为( )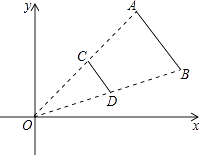 A、(3,3) B、(4,3) C、(3,1) D、(4,1)7. 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的 ,设人行通道的宽度为x千米,则下列方程正确的是( )
A、(3,3) B、(4,3) C、(3,1) D、(4,1)7. 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的 ,设人行通道的宽度为x千米,则下列方程正确的是( ) A、(2﹣3x)(1﹣2x)=1 B、 (2﹣3x)(1﹣2x)=1 C、 (2﹣3x)(1﹣2x)=1 D、 (2﹣3x)(1﹣2x)=28. 为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A、(2﹣3x)(1﹣2x)=1 B、 (2﹣3x)(1﹣2x)=1 C、 (2﹣3x)(1﹣2x)=1 D、 (2﹣3x)(1﹣2x)=28. 为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A、5,5, B、5,5,10 C、6,5.5, D、5,5,9. 一个不透明的袋子中装有4张卡片,卡片上分别标有数字﹣3,1, ,2,它们除所标数字外完全相同,摇匀后从中随机摸出两张卡片,则两张卡片上所标数字之积是正数的概率是( )A、 B、 C、 D、10. 如图,点C是⊙O上一点,⊙O的半径为 ,D、E分别是弦AC、BC上一动点,且OD=OE= ,则AB的最大值为( )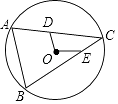 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 使式子 有意义的x的取值范围是 .12. 已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x时,y≤0.13. 若关于x的方程x2﹣6x+m=0有两个相等的实数根,则实数m= .14. 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④4a﹣2b+c>0,其中正确的个数为 .
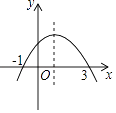 15. 如图,直径为10的⊙A经过点C(0,5)和点0(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为 .
15. 如图,直径为10的⊙A经过点C(0,5)和点0(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为 .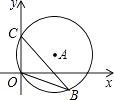
三、解答题
-
16. 先化简,再求值: ÷(a﹣1+ ),其中a是方程x2﹣x=6的根.17. 如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明.
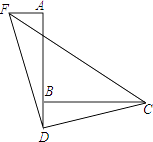 18. 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE.
18. 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE.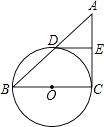 (1)、若AD=DB,OC=5,求切线AC的长;(2)、求证:ED是⊙O的切线.19. “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
(1)、若AD=DB,OC=5,求切线AC的长;(2)、求证:ED是⊙O的切线.19. “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表: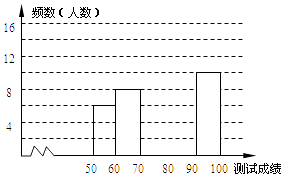
请结合图表完成下列各题:
(1)、①表中a的值为 , 中位数在第组;②频数分布直方图补充完整;
(2)、若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?(3)、第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
20. 如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处. (1)、求该轮船航行的速度;(2)、如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据: , )21. 某玩具厂生产一种玩具,据市场调查,若按每个玩具280元销售时,每月可销售300个,若销售单价每降低1元,每月可多售出2个,据统计,每个玩具的固定成本Q(元)与月销量y(个)满足如下关系:
(1)、求该轮船航行的速度;(2)、如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据: , )21. 某玩具厂生产一种玩具,据市场调查,若按每个玩具280元销售时,每月可销售300个,若销售单价每降低1元,每月可多售出2个,据统计,每个玩具的固定成本Q(元)与月销量y(个)满足如下关系:月销量y(个)
…
160
200
240
300
…
每个玩具的固定成本Q(元)
…
60
48
40
32
…
(1)、写出月销量y(个)与销售单价x(元)之间的函数关系式;
(2)、求每个玩具的固定成本Q(元)与月销量y(个)之间的函数关系式;
(3)、若每个玩具的固定成本为30元,则它占销售单价的比例是多少?(用分数表示)(4)、若该厂这种玩具的月销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?22. 综合题:解答下列问题.
(1)、问题发现,如图1,在正方形ABCD中,点E为CD的中点,过点D作AE的垂线,垂足为F与AC、BC分别交于点G,点H,则 = .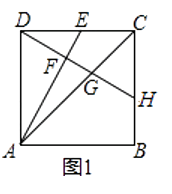 (2)、类比探究;如图2,在矩形ABCD中, = ,点E为CD的中点,过点D作AE的垂线,垂足为F,与AC、BC分别交于点G,点H,试探究 的值,并写出推理过程.
(2)、类比探究;如图2,在矩形ABCD中, = ,点E为CD的中点,过点D作AE的垂线,垂足为F,与AC、BC分别交于点G,点H,试探究 的值,并写出推理过程. 23. 如图,抛物线经过A(﹣1,0),B(5,0),C(0, )三点.
23. 如图,抛物线经过A(﹣1,0),B(5,0),C(0, )三点. (1)、求抛物线的解析式;(2)、在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)、点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)、点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.