贵州省黔南州平塘二中2017年中考数学四模试卷
试卷更新日期:2017-11-09 类型:中考模拟
一、选择题
-
1. 下列各对数中,互为相反数的是( )A、﹣(+5)和﹣5 B、+(﹣5)和﹣5 C、﹣ 和﹣(+ ) D、+|+8|和﹣(+8)2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为( )
3. 我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为( ) A、5.5×106千米 B、5.5×107千米 C、55×106千米 D、0.55×108千米4. 从只装有4个红球的袋中随机摸出一球,若摸到白球的概率是p1 , 摸到红球的概率是p2 , 则( )A、p1=1,p2=1 B、p1=0,p2=1 C、p1=0,p2= D、p1=p2=5. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
A、5.5×106千米 B、5.5×107千米 C、55×106千米 D、0.55×108千米4. 从只装有4个红球的袋中随机摸出一球,若摸到白球的概率是p1 , 摸到红球的概率是p2 , 则( )A、p1=1,p2=1 B、p1=0,p2=1 C、p1=0,p2= D、p1=p2=5. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )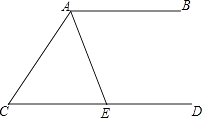 A、65° B、115° C、125° D、130°6. 一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )A、3,3,0.4 B、2,3,2 C、3,2,0.4 D、3,3,27. 如果 =2﹣x,那么( )A、x<2 B、x≤2 C、x>2 D、x≥28. 将抛物线y=x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( )A、y=(x+2)2﹣3 B、y=(x+2)2+3 C、y=(x﹣2)2+3 D、y=(x﹣2)2﹣39. 已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( )A、 B、 C、 D、不能确定10. 当k>0时,反比例函数y= 和一次函数y=kx+2的图象大致是( )A、
A、65° B、115° C、125° D、130°6. 一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )A、3,3,0.4 B、2,3,2 C、3,2,0.4 D、3,3,27. 如果 =2﹣x,那么( )A、x<2 B、x≤2 C、x>2 D、x≥28. 将抛物线y=x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( )A、y=(x+2)2﹣3 B、y=(x+2)2+3 C、y=(x﹣2)2+3 D、y=(x﹣2)2﹣39. 已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( )A、 B、 C、 D、不能确定10. 当k>0时,反比例函数y= 和一次函数y=kx+2的图象大致是( )A、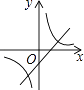 B、
B、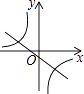 C、
C、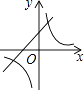 D、
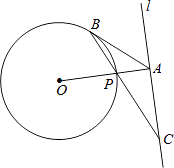
D、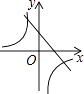 11. 如图,△ABC内接于⊙O,CD是⊙O的直径,∠A=35°,则∠BCD的度数是( )
11. 如图,△ABC内接于⊙O,CD是⊙O的直径,∠A=35°,则∠BCD的度数是( )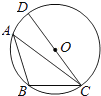 A、55° B、65° C、70° D、75°12. 如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是( )
A、55° B、65° C、70° D、75°12. 如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是( )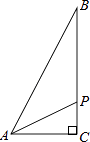 A、
A、 B、
B、 C、
C、 D、
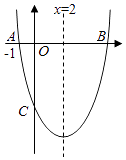
D、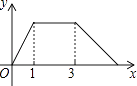 13. 如图是二次函数y=ax2+bx+c过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac,②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( )
13. 如图是二次函数y=ax2+bx+c过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac,②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( ) A、②④ B、①④ C、②③ D、①③
A、②④ B、①④ C、②③ D、①③二、填空题
-
14. 计算(﹣1)2005﹣| ﹣2|+(﹣ )﹣1﹣2sin60°的值为 .15. 如图,在△ABC中,∠C=90°,AD平分∠CAB,AC=6cm,AB=10cm,那么D点到直线AB的距离是 cm.
 16. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.
16. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm. 17. 如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若 ,则 = .
17. 如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若 ,则 = . 18. 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果精确到0.1米,参考数据: =1.41, =1.73).
18. 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为米(结果精确到0.1米,参考数据: =1.41, =1.73).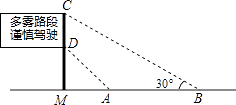 19.
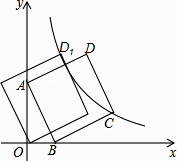
19.如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= (k≠0)上的点D1处,则a= .
三、简答题
-
20. 计算:
(1)、解方程组:;(2)、化简 ÷(x+2﹣ ).21. 如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,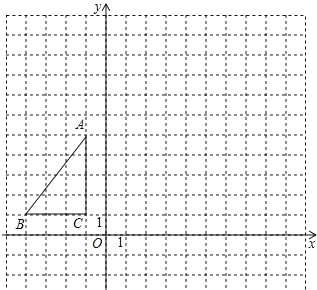 (1)、画出△AB′C′;
(1)、画出△AB′C′;
(2)、写出点B′,C′的坐标;
(3)、求出在△ABC旋转的过程中,点C经过的路径长.
22. 为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,以便国家精准扶贫政策有效落实.统计发现班上贫困家庭学生人数分别有2名、3名、4名、5名、6名,共五种情况.并将其制成了如下两幅不完整的统计图: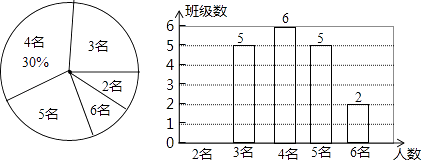 (1)、求该校一共有多少个班?并将条形图补充完整;(2)、某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表法或树状图的方法,求出被选中的两名学生来自同一班级的概率.23. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求:
(1)、求该校一共有多少个班?并将条形图补充完整;(2)、某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表法或树状图的方法,求出被选中的两名学生来自同一班级的概率.23. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求: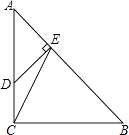 (1)、线段BE的长;
(1)、线段BE的长;
(2)、∠ECB的余切值.
24. 现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)、请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)、小明选择哪家快递公司更省钱?