贵州省黔南州平塘二中2017年中考数学二模试卷
试卷更新日期:2017-11-09 类型:中考模拟
一、选择题
-
1. ﹣5的倒数的相反数是( )A、5 B、 C、﹣5 D、2. 下列运算正确的是( )A、x•x2=x2 B、(xy)2=xy2 C、(x2)3=x6 D、x2+x2=x43. 一组数据2、5、4、3、5、4、5的中位数和众数分别是( )A、3.5,5 B、4,4 C、4,5 D、4.5,44. 从1~9这九个自然数中任取一个,是2的倍数的概率是( )A、 B、 C、 D、5.
如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )
 A、3 B、4 C、6 D、86. 如图是由我市某中学楼层间的两个台阶组成的几何体,已知两个台阶的高度和宽度是相同的,据此可判断此几何体的三视图是( )
A、3 B、4 C、6 D、86. 如图是由我市某中学楼层间的两个台阶组成的几何体,已知两个台阶的高度和宽度是相同的,据此可判断此几何体的三视图是( ) A、
A、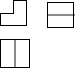 B、
B、 C、
C、 D、
D、 7. 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
7. 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( ) A、40° B、50° C、60° D、30°8. 如图,在△ABC中,AB=AC,AB=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
A、40° B、50° C、60° D、30°8. 如图,在△ABC中,AB=AC,AB=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( ) A、 B、16π﹣32 C、 D、9. 下列命题正确的个数有( )
A、 B、16π﹣32 C、 D、9. 下列命题正确的个数有( )①相等的圆周角所对的弧相等;
②圆的两条平行弦所夹的弧相等;
③三点确定一个圆;
④在同圆或等圆中,同弦或等弦所对的圆周角相等或互补.
A、1 B、2 C、3 D、410. 若分式 有意义,则x的取值范围是( )A、x> B、x≤ 且x≠0 C、x≥ D、x> 且x≠011. 已知反比例函数y= , 下列结论不正确的是( )A、图象经过点(1,1) B、图象在第一、三象限 C、当x>1时,0<y<1 D、当x<0时,y随着x的增大而增大12. 抛物线图象如图所示,根据图象,抛物线的解析式可能是( ) A、y=x2﹣2x+3 B、y=﹣x2﹣2x+3 C、y=﹣x2+2x+3 D、y=﹣x2+2x﹣313. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
A、y=x2﹣2x+3 B、y=﹣x2﹣2x+3 C、y=﹣x2+2x+3 D、y=﹣x2+2x﹣313. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.
其中正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
14. 分解因式:x2+4+4x﹣y2= .
15. 如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE= . 16. 如图,已知⊙P的半径为2,圆心P在抛物线y= ﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为 .
16. 如图,已知⊙P的半径为2,圆心P在抛物线y= ﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为 . 17. 观察下列等式:
17. 观察下列等式:
在上述数字宝塔中,从上往下数,2016在第层.
18. 如图,在▱ABCD中,点E在边BC上,BE:EC=1:2,连接AE交BD于点F,则△BFE的面积与△DFA的面积之比为 . 19. 如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为 .
19. 如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为 .
三、解答题
-
20. 计算:
(1)、(﹣)﹣1﹣|﹣ 3 |﹣20110+( 2 )2+tan60°;
(2)、解分式方程: ﹣ = .
21. 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.
试问:
(1)、图中△APD与哪个三角形全等?并说明理由.(2)、求证:PA2=PE•PF.22. 我省某地区为了了解2016年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如图1,如图2)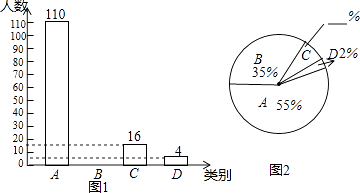 (1)、填空:该地区共调查了名九年级学生;(2)、将两幅统计图中不完整的部分补充完整;(3)、若该地区2016年初中毕业生共有3500人,请估计该地区今年初中毕业生中读普通高中的学生人数;(4)、老师想从甲,乙,丙,丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用画树状图或列表的方法求选中甲同学的概率.23. 如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B,F,C在一条直线上)
(1)、填空:该地区共调查了名九年级学生;(2)、将两幅统计图中不完整的部分补充完整;(3)、若该地区2016年初中毕业生共有3500人,请估计该地区今年初中毕业生中读普通高中的学生人数;(4)、老师想从甲,乙,丙,丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用画树状图或列表的方法求选中甲同学的概率.23. 如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B,F,C在一条直线上) (1)、求教学楼AB的高度;(2)、学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(1)、求教学楼AB的高度;(2)、学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).(参考数据:sin22°≈ ,cos22°≈ ,tan22°≈ )
24. 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD= . (1)、求证:CD∥BF;(2)、求⊙O的半径;(3)、求弦CD的长.25. 某校组织学生到外地进行社会实践活动,共有680名学生参加,并携带300件行李.学校计划租用甲、乙两种型号的汽车共20辆.经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.(1)、如何安排甲、乙两种汽车可一次性地将学生和行李全部运走?有哪几种方案?(2)、如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案.26. 如图,已知抛物线y=x2﹣ax+a2﹣4a﹣4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿直线CD运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿直线AB运动,连接PQ,CB,PB,设点P运动的时间为t秒.
(1)、求证:CD∥BF;(2)、求⊙O的半径;(3)、求弦CD的长.25. 某校组织学生到外地进行社会实践活动,共有680名学生参加,并携带300件行李.学校计划租用甲、乙两种型号的汽车共20辆.经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.(1)、如何安排甲、乙两种汽车可一次性地将学生和行李全部运走?有哪几种方案?(2)、如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案.26. 如图,已知抛物线y=x2﹣ax+a2﹣4a﹣4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿直线CD运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿直线AB运动,连接PQ,CB,PB,设点P运动的时间为t秒. (1)、求a的值;(2)、当四边形ODPQ为矩形时,求这个矩形的面积;(3)、当四边形PQBC的面积等于14时,求t的值.(4)、当t为何值时,△PBQ是等腰三角形?(直接写出答案)
(1)、求a的值;(2)、当四边形ODPQ为矩形时,求这个矩形的面积;(3)、当四边形PQBC的面积等于14时,求t的值.(4)、当t为何值时,△PBQ是等腰三角形?(直接写出答案)