广东省2017年中考数学押题试卷
试卷更新日期:2017-11-09 类型:中考模拟
一、选择题
-
1. ﹣2017的相反数是( )A、﹣2017 B、2017 C、﹣ D、2. 数据7、7、5、5、6、5、6的众数是( )A、0 B、7 C、6 D、53. 不等式5x﹣5>2x+1的解集在数轴上表示正确的是( )A、
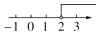 B、
B、 C、
C、 D、
D、 4. 如图,是由几个相同的小正方体组成的一个几何体的三视图,这个几何体可能是( )
4. 如图,是由几个相同的小正方体组成的一个几何体的三视图,这个几何体可能是( )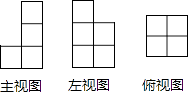 A、
A、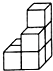 B、
B、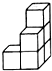 C、
C、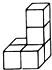 D、
D、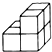 5. 在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为( )A、 B、 C、 D、6. 如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( )
5. 在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为( )A、 B、 C、 D、6. 如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( ) A、30° B、45° C、55° D、60°7. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°8. 已知3是方程x2﹣mx+n=0的一个根,则3﹣ m+ n=( )
A、30° B、45° C、55° D、60°7. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°8. 已知3是方程x2﹣mx+n=0的一个根,则3﹣ m+ n=( )
A、2 B、3 C、4 D、59. 如图为4×4的网格图,A,B,C,D,O均在格点上,点O是( )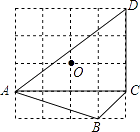 A、△ACD的外心 B、△ABC的外心 C、△ACD的内心 D、△ABC的内心10. 如图,等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t.则大致反映S与t变化关系的图象是( )
A、△ACD的外心 B、△ABC的外心 C、△ACD的内心 D、△ABC的内心10. 如图,等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t.则大致反映S与t变化关系的图象是( )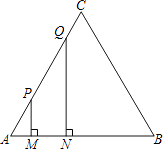 A、
A、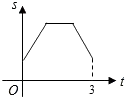 B、
B、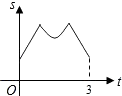 C、
C、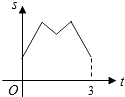 D、
D、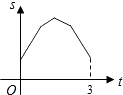
二、填空题
-
11. 地球上的海洋面积大约为361000000千米2 , 将361000000这个数用科学记数法表示为 .12. 要使式子 有意义,则x可以取的最小整数是 .
13. 若实数a、b满足|a﹣2|+ =0,则ba= .
14. 若两个相似多边形面积比为4:9,则它们的周长比是 .15. 如图,在菱形ABCD中,AC=8,BD=6,则△AOB的周长等于 .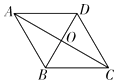 16. 矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△AEF的面积等于 .
16. 矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△AEF的面积等于 .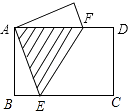
三、解答题
-
17. 计算: ﹣(π﹣2017)0+| ﹣2|+2sin60°.
18. 先化简,再求值:(x﹣ )÷ ,其中x= .19. 如图,点A,C分别在∠XOY的边OX和OY上,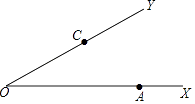 (1)、尺规作图:在OY的右侧作∠YCP=∠YOA;(不写作法,保留痕迹).(2)、在射线CP上取一点B,使CB=OA,连接AB,问:四边形 OABC是什么四边形?
(1)、尺规作图:在OY的右侧作∠YCP=∠YOA;(不写作法,保留痕迹).(2)、在射线CP上取一点B,使CB=OA,连接AB,问:四边形 OABC是什么四边形?四、解答题
-
20. “校园手机”现象越来越受到社会的关注,小记者小明 随机调查了某校若干学生和家长对中学生
带手机现象的看法,制作了如下不完整的统计图:
 (1)、求这次调查的总人数(学生和家长),并补全图1;(2)、求图2中表示家长“赞成”的圆心角的度数;
(1)、求这次调查的总人数(学生和家长),并补全图1;(2)、求图2中表示家长“赞成”的圆心角的度数;
(3)、针对随机调查的情况,小明决定从九年级(一)班表示赞成的3位家长(其中包含小亮和小丁的家长)中随机选择2位进行深入调查,请你利用树状图或列表的方法,求出小亮和小丁的家长被同时选中的概率.
21. 某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)、求该种商品每次降价的百分率;(2)、若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?
22. 某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面AC的坡度为1: . (1)、求新坡面AC的坡角∠CAB;
(1)、求新坡面AC的坡角∠CAB;
(2)、原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆桥?请说明理由.
五、解答题
-
23. 如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
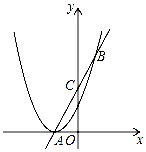 (1)、求这条抛物线对应的函数解析式;
(1)、求这条抛物线对应的函数解析式;
(2)、求直线AB对应的函数解析式;
(3)、若点D在x轴上,且△ACD是等腰三角形,请直接写出D点的坐标.
24. 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C. (1)、求证:PE是⊙O的切线;
(1)、求证:PE是⊙O的切线;
(2)、求证:ED平分∠BEP;
(3)、若⊙O的半径为5,CF=2EF,求PD的长.
25. 如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题: (1)、当t= 时,则 =; =; 此时EP与AB的位置关系是;(2)、连接PF,证明:PE=PF;
(1)、当t= 时,则 =; =; 此时EP与AB的位置关系是;(2)、连接PF,证明:PE=PF;
(3)、设△PEQ的面积为y(cm2),求y与t之间的函数关系式.
26. 如图,直线y=﹣x+4与两坐标轴分别相交于A,B点,点M是线段AB上任意一点(A,B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D. (1)、当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化并说明理由;
(1)、当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化并说明理由;
(2)、当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)、当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为a(0<a<4),正方形OCMD与△AOB重叠部分的面积为S.试求S与a的函数关系式并画出该函数的图象.