2015-2016学年江苏省泰州市兴化市顾庄学区三校八年级下学期第一次月考数学试卷

试卷更新日期：2016-08-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 既是中心对称图形，又是轴对称图形的是（　　）

A、平行四边形 B、正五边形 C、菱形 D、等腰梯形

查看试题解析
2. 下列说法正确的是（　　）

A、“购买一张彩票就中奖”是不可能事件 B、“抛掷一枚质地均匀的骰子，向上一面的点数是6”是随机事件 C、了解我国青年人喜欢的电视节目应做普查 D、从扇形统计图中，可以直接得到各部分的具体数值

查看试题解析
3. 如图，在▱ABCD中，下列结论错误的是（）

A、∠ABD=∠BDC B、∠BAD=∠BCD C、AB=CD D、AC⊥BD

查看试题解析
4. 若反比例函数y= $\frac{k}{x}$ 的图象经过点（2，﹣1），则该反比例函数的图象在（　　）

A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限

查看试题解析
5. 如图，▱ABCD的对角线AC，BD相交于点O，下列条件可使的▱ABCD为菱形的是（）

A、AC=BD B、∠DAB=∠DCB C、AD=BC D、∠AOD=90°

查看试题解析
6.
如图，一次函数与反比例函数的图象相交于A、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是（　　）

A、x＜﹣1 B、x＞2 C、x＜﹣1或0＜x＜2 D、﹣1＜x＜0或x＞2

查看试题解析

二、填空题

7. 一次数学测验，100名学生中有25名得了优秀，则优秀人数的频率是．

查看试题解析
8. 当x= 时，分式 $\frac{x + 1}{x - 2}$ 的值为0．

查看试题解析
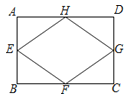
9. 在函数y= $\sqrt{x - 4}$ 中，自变量x的取值范围是

查看试题解析
10. 已知点（1，﹣2）在反比例函数y= $\frac{k}{x}$ 的图象上，则k=

查看试题解析
11. 关于x的分式方程 $\frac{m}{x + 1}$ =﹣1的解是负数，则m的取值范围是

查看试题解析
12.
如图，已知矩形ABCD的对角线长为8cm，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长等于cm．

查看试题解析
13. 若反比例函数 $y = (m + 1) x^{3 - m^{2}}$ 的图象在第二、四象限，m的值为

查看试题解析
14. 若关于x方程 $\frac{a}{x - 2}$ = $\frac{4}{x - 2}$ +1无解，则a的值为

查看试题解析
15. 在一个不透明的袋子中装有仅颜色不同的10个小球，其中红球4个，黑球6个，先从袋子取出m个红球，再放入m个一样的黑球并摇匀，随机摸出一个球是黑球的概率等于 $\frac{4}{5}$ ，则m的值为

查看试题解析
16. 已知反比例函数y=﹣ $\frac{8}{x}$ ，则有
①它的图象在一、三象限：
②点（﹣2，4）在它的图象上；
③当l＜x＜2时，y的取值范围是﹣8＜y＜﹣4；
④若该函数的图象上有两个点A （x₁ ， y₁），B（x₂ ， y₂），那么当x₁＜x₂时，y₁＜y₂
以上叙述正确的是

查看试题解析

三、解答题

17. 解方程
（1） $\frac{3 + x}{4 - x} = \frac{1}{2}$
（2） $\frac{1}{x - 2} = \frac{1 - x}{2 - x} - 3$ ．

查看试题解析
18. 先化简，再求值：（1+ $\frac{1}{a^{2} - 1}$ ）÷ $\frac{a}{3 (a + 1)}$ ，其中a=4．

查看试题解析
19. 某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同，现在平均每天生产多少台机器？

查看试题解析
20.
在▱ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．
（1）求证：四边形BFDE是矩形；
（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．

查看试题解析
21.
某课题组为了解全市九年级学生对数学知识的掌握情况，在一次数学检测中，从全市24000名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如下图表：
分数段
频数
频率
x＜60
20
0.10
60≤x＜70
28
0.14
70≤x＜80
54
0.27
80≤x＜90
a
0.20
90≤x＜100
24
0.12
100≤x＜110
18
b
110≤x＜120
16
0.08
请根据以上图表提供的信息，解答下列问题：
（1）表中a和b所表示的数分别为多少；
（2）请在图中，补全频数分布直方图；

（3）如果把成绩在90分以上（含90分）定为优秀，那么该市24000名九年级考生数学成绩为优秀的学生约有多少名？

查看试题解析
22. 某乡镇要在生活垃圾存放区建一个老年活动中心，这样必须把1200立方米的生活垃圾运走：
（1）假如每天能运x立方米，所需时间为y天，写出y与x之间的函数表达式；
（2）若每辆拖拉机一天能运12立方米，则5辆这样的拖拉机要用多少天才能运完？
（3）在（2）的情况下，运了8天后，剩下的任务要在不超过6天的时间内完成，那么至少需要增加多少辆这样的拖拉机才能按时完成任务？

查看试题解析
23.
如图，在Rt△ABC中，∠BAC=90°，E，F分别是BC，AC的中点，延长BA到点D，使AD= $\frac{1}{2}$ AB．连接DE，DF．
（1）求证：AF与DE互相平分；
（2）若BC=4，求DF的长．

查看试题解析
24. 已知反比例函数y= $\frac{k}{x}$ （k为常数，k≠0）的图象经过点A（2，3）．
（Ⅰ）求这个函数的解析式；
（Ⅱ）判断点B（﹣1，6），C（3，2）是否在这个函数的图象上，并说明理由；
（Ⅲ）当﹣3＜x＜﹣1时，求y的取值范围．

查看试题解析
25.
在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F
（1）求证：△AEF≌△DEB；
（2）证明：四边形ADCF是菱形；
（3）若AB=4，AC=5，求菱形ADCF的面积．

查看试题解析
26.
如图，已知A（﹣4， $\frac{1}{2}$ ），B（﹣1，2）是一次函数y=kx+b与反比例函数y= $\frac{m}{x}$ （m≠0，x＜0）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D．
（1）根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值？
（2）求一次函数解析式及m的值；
（3）P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标．

查看试题解析

分数段	频数	频率
x＜60	20	0.10
60≤x＜70	28	0.14
70≤x＜80	54	0.27
80≤x＜90	a	0.20
90≤x＜100	24	0.12
100≤x＜110	18	b
110≤x＜120	16	0.08