2016年广东省梅州市中考数学试卷

试卷更新日期：2016-08-08 类型：中考真卷

进入出卷网下载

一、选择题：

1. 计算：（﹣3）+4的结果是（　　）

A、﹣7 B、﹣1 C、1 D、7

查看试题解析
2. 若一组数据3，x，4，5，6的众数是3，则这组数据的中位数为（　　）

A、3 B、4 C、5 D、6

查看试题解析
3.
如图，几何体的俯视图是（　　）

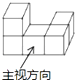A、 B、 C、 D、

查看试题解析
4. 分解因式a²b﹣b³结果正确的是（　　）

A、b（a+b）（a﹣b） B、b（a﹣b）² C、b（a²﹣b²） D、b（a+b）²

查看试题解析
5.
如图，BC⊥AE于点C，CD∥AB，∠B=55°，则∠1等于（　　）

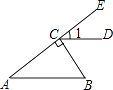A、55° B、45° C、35° D、25°

查看试题解析
6. 二次根式 $\sqrt{2 - x}$ 有意义，则x的取值范围是（　　）

A、x＞2 B、x＜2 C、x≥2 D、x≤2

查看试题解析
7. 对于实数a、b，定义一种新运算“⊗”为：a⊗b= $\frac{1}{a - b^{2}}$ ，这里等式右边是实数运算．例如：1⊗3= $\frac{1}{1 - 3^{2}} = - \frac{1}{8}$ ．则方程x⊗（﹣2）= $\frac{2}{x - 4}$ ﹣1的解是（　　）

A、x=4 B、x=5 C、x=6 D、x=7

查看试题解析

二、填空题：

8. 比较大小：﹣2﹣3．

查看试题解析
9. 在一个不透明的口袋中，装有若干个除颜色不同外，其余都相同的小球．如果口袋中装有3个红球且从中随机摸出一个球是红球的概率为 $\frac{1}{5}$ ，那么口袋中小球共有个．

查看试题解析
10. 流经我市的汀江，在青溪水库的正常库容是6880万立方米.6880万用科学记数法表示为．

查看试题解析
11. 已知点P（3﹣m，m）在第二象限，则m的取值范围是．

查看试题解析
12. 用一条长40cm的绳子围成一个面积为64cm²的矩形．设矩形的一边长为xcm，则可列方程为．

查看试题解析
13.
如图，在平行四边形ABCD中，点E是边AD的中点，EC交对角线BD于点F，若S_△_DEC=3，则S_△_BCF= ．

查看试题解析
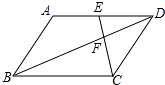14.
如图，抛物线y=﹣x²+2x+3与y轴交于点C，点D（0，1），点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为．

查看试题解析
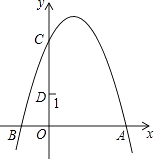15.
如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB₁C₁的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去…．若点A（ $\frac{3}{2}$ ，0），B（0，2），则点B₂₀₁₆的坐标为．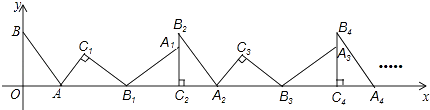

查看试题解析

三、解答下列各题：

16. 计算： ${(π - 5)}^{0} + \sqrt{2} \cos 45^{0} - | - 3 | + {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
17. 我市某校开展了以“梦想中国”为主题的摄影大赛，要求参赛学生每人交一件作品．现将从中挑选的50件参赛作品的成绩（单位：分）统计如下：
等级
成绩（用m表示）
频数
频率
A
90≤m≤100
x
0.08
B
80≤m＜90
34
y
C
m＜80
12
0.24
合计

50
1
请根据上表提供的信息，解答下列问题：

(1)、表中x的值为， y的值为；（直接填写结果）

(2)、将本次参赛作品获得A等级的学生依次用A₁、A₂、A₃…表示．现该校决定从本次参赛作品获得A等级的学生中，随机抽取两名学生谈谈他们的参赛体会，则恰好抽到学生A₁和A₂的概率为．（直接填写结果）

查看试题解析
18.
如图，在平行四边形ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于 $\frac{1}{2}$ BF长为半径画弧，两弧交于一点P，连
接AP并延长交BC于点E，连接EF．

(1)、四边形ABEF是；（选填矩形、菱形、正方形、无法确定）（直接填写结果）

(2)、AE，BF相交于点O，若四边形ABEF的周长为40，BF=10，则AE的长为， ∠ABC=°．（直接填写结果）

查看试题解析
19.
如图，已知在平面直角坐标系中，O是坐标原点，点A（2，5）在反比例函数y= $\frac{k}{x}$ 的图象上．一次函数y=x+b的图象过点A，且与反比例函数图象的另一交点为B．

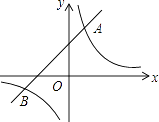(1)、求k和b的值；

(2)、设反比例函数值为y₁ ，一次函数值为y₂ ，求y₁＞y₂时x的取值范围．

查看试题解析
20.
如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°．

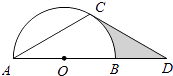(1)、求证：CD是⊙O的切线；

(2)、若⊙O的半径为2，求图中阴影部分的面积．

查看试题解析
21. 关于x的一元二次方程x²+（2k+1）x+k²+1=0有两个不等实根x₁、x₂ ．

(1)、求实数k的取值范围．

(2)、若方程两实根x₁、x₂满足x₁+x₂=﹣x₁•x₂ ，求k的值．

查看试题解析
22.
如图，平行四边形ABCD中，BD⊥AD，∠A=45°，E、F分别是AB、CD上的点，且BE=DF，连接EF交BD于O．

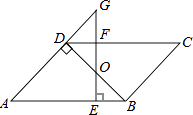(1)、求证：BO=DO；

(2)、若EF⊥AB，延长EF交AD的延长线于G，当FG=1时，求AE的长．

查看试题解析
23.
如图，在Rt△ABC中，∠ACB=90°，AC=5cm，∠BAC=60°，动点M从点B出发，在BA边上以每秒2cm的速度向点A匀速运动，同时动点N从点C出发，在CB边上以每秒 $\sqrt{3}$ cm的速度向点B匀速运动，设运动时间为t秒（0≤t≤5），连接MN．

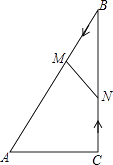(1)、若BM=BN，求t的值；

(2)、若△MBN与△ABC相似，求t的值；

(3)、当t为何值时，四边形ACNM的面积最小？并求出最小值．

查看试题解析
24.
如图，在平面直角坐标系中，已知抛物线y=x²+bx+c过A，B，C三点，点A的坐标是（3，0），点C的坐标是（0，﹣3），动点P在抛物线上．

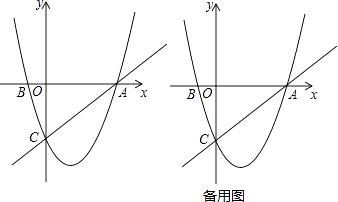(1)、b= ， c= ，点B的坐标为；（直接填写结果）

(2)、是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

(3)、过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．

查看试题解析

等级	成绩（用m表示）	频数	频率
A	90≤m≤100	x	0.08
B	80≤m＜90	34	y
C	m＜80	12	0.24
合计		50	1