黑龙江省大庆市林甸四中2017年中考数学三模试
试卷更新日期:2017-11-07 类型:中考模拟
一、选择题
-
1. 下列计算正确的是( )A、2a+3b=5ab B、(﹣2a2b)3=﹣6a6b3 C、 + =3 D、(a+b)2=a2+b22. 如图,所给图形中是中心对称图形但不是轴对称图形的是( )A、
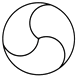 B、
B、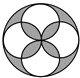 C、
C、 D、
D、 3. 若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )A、矩形 B、菱形 C、对角线相等的四边形 D、对角线互相垂直的四边形4. 从长度分别为1、3、5、7的四条线段中任选三条作边,能构成三角形的概率为 ( )A、 B、 C、 D、5. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
3. 若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )A、矩形 B、菱形 C、对角线相等的四边形 D、对角线互相垂直的四边形4. 从长度分别为1、3、5、7的四条线段中任选三条作边,能构成三角形的概率为 ( )A、 B、 C、 D、5. 如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )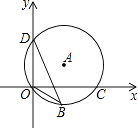 A、 B、 C、 D、6. 将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、360° B、540° C、720° D、900°7. 如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y= 交于E,F两点,若AB=2EF,则k的值是( )
A、 B、 C、 D、6. 将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、360° B、540° C、720° D、900°7. 如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y= 交于E,F两点,若AB=2EF,则k的值是( ) A、﹣1 B、1 C、 D、8. 二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数 与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
A、﹣1 B、1 C、 D、8. 二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数 与一次函数y=bx﹣c在同一坐标系内的图象大致是( ) A、
A、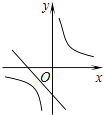 B、
B、 C、
C、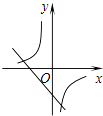 D、
D、 9. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
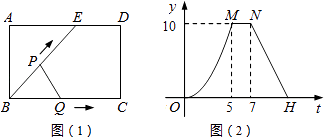
9. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( ) A、84 B、336 C、510 D、132610. 如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分),则下列结论:
A、84 B、336 C、510 D、132610. 如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5cm;②当0<t≤5时,y= t2;③直线NH的解析式为y=﹣ t+27;④若△ABE与△QBP相似,则t= 秒,
其中正确结论的个数为( )
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 要使代数式 有意义,则x的取值范围是 .12. 据报载,2016年我国发展固定宽带接入新用户260000000户,其中260000000用科学记数法表示为 .13. 已知 是二元一次方程组 的解,则2n﹣m的平方根是 .
14. 对于任意实数m、n,定义一种运算m※n=mn﹣m﹣n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5﹣3﹣5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是 .15. 已知关于x的分式方程 + =1的解是非负数,则a的取值范围是 .
16. 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是 cm.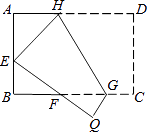 17. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转α角后得到△A′B′C,当点A的对应点A'落在AB边上时,旋转角α的度数是度,阴影部分的面积为 .
17. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转α角后得到△A′B′C,当点A的对应点A'落在AB边上时,旋转角α的度数是度,阴影部分的面积为 . 18.
18.如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从4这点开始跳,则经2015次跳后它停在数对应的点上.

三、解答题
-
19. 计算: ﹣sin60°+ × .20. 先化简,再求值:( ﹣ )÷ ,其中x是方程3x2﹣x﹣1=0的根.
21. 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).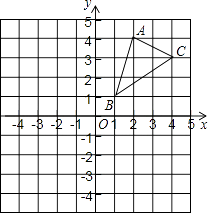
①请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;
②请画出△ABC绕点B逆时针旋转90°后的△A2BC2 , 并写出点A2、C2的坐标.
22. 已知关于x的方程x2+3x+ =0有两个不相等的实数根.(1)、求m的取值范围;
(2)、若m为符合条件的最大整数,求此时方程的根.23. 如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC. (1)、求证:DE是圆O的切线;(2)、若∠C=30°,CD=10cm,求圆O的半径.24. 学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.
(1)、求证:DE是圆O的切线;(2)、若∠C=30°,CD=10cm,求圆O的半径.24. 学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图. (1)、学校采用的调查方式是;学校共选取了名学生;(2)、补全统计图中的数据:条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他 %;(3)、该校共有1200名学生,请估计喜欢“乒乓球”的学生人数.25. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)、学校采用的调查方式是;学校共选取了名学生;(2)、补全统计图中的数据:条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他 %;(3)、该校共有1200名学生,请估计喜欢“乒乓球”的学生人数.25. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.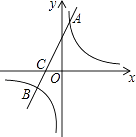 (1)、求该反比例函数和一次函数的解析式;(2)、求点B的坐标.
(1)、求该反比例函数和一次函数的解析式;(2)、求点B的坐标.
26. 在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x (元)的一次函数.(1)、直接写出y与x之间的函数关系式y= .(2)、在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?27. 以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.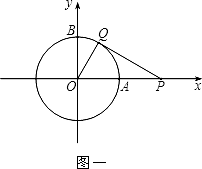
 (1)、如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是⊙O的切线,连接OQ.求∠QOP的大小;(2)、若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被⊙O截得的弦长.28. 已知抛物线y=﹣ +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
(1)、如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是⊙O的切线,连接OQ.求∠QOP的大小;(2)、若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被⊙O截得的弦长.28. 已知抛物线y=﹣ +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0). (1)、求抛物线的解析式;(2)、已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;(3)、已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;(3)、已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.