2015-2016学年江苏省扬州市江都二中七年级下学期第一次月考数学试卷

试卷更新日期：2016-08-08 类型：月考试卷

进入出卷网下载

一、单选题

1. 下面3个命题：①同旁内角互补；②两直线平行，内错角相等；③在同一平面内，垂直于同一直线的两直线互相平行，其中真命题为（　　）

A、① B、③ C、②③ D、②

查看试题解析
2. 下列计算正确的是（　　）

A、a+a²=2a³ B、a²•a³=a⁶ C、（2a⁴）⁴=16a⁸ D、（﹣a）⁶÷a³=a³

查看试题解析
3. 如图，在平行四边形ABCD中，CE⊥AB且E为垂足．如果∠A=125°，则∠BCE=（）

A、55° B、35° C、25° D、30°

查看试题解析
4. 把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为（）

A、125° B、120° C、140° D、130°

查看试题解析
5. 计算25^m÷5^m的结果为（　　）

A、5 B、 $5^{m}$ C、20 D、 $20^{m}$

查看试题解析
6. 有5条线段，它们的长度分别为1cm，2cm，3cm，4cm，5cm，以其中三条线段为边长，可组成不同的三角形的个数为（　　）

A、3 B、4 C、5 D、6

查看试题解析
7. 如图，过正五边形ABCDE的顶点A作直线l∥BE，则∠1的度数为（）

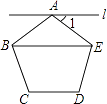A、30° B、36° C、38° D、45°

查看试题解析
8.
如图，四边形ABCD中，点M ， N分别在AB ， BC上，将△BMN沿MN翻折，得△FMN ，若MF∥AD ， FN∥DC ，则∠B =（　　）

A、95° B、90° C、135° D、120°

查看试题解析

二、填空题

9. 一个多边形的每个外角都是60°，则这个多边形边数为

查看试题解析
10. PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．某天灌南县城区的PM2.5值是29微克/立方米，根据PM2.5检测网的空气质量新标准，这一天城区的PM2.5值为优，请用科学记数法表示：2.5微米=米．（1米=1000000微米）

查看试题解析
11. 已知a=﹣（0.2）² ， b=﹣2^﹣2 ， c=（﹣ $\frac{1}{2}$ ）^﹣2 ， d=（﹣ $\frac{1}{2}$ ）⁰ ，则比较a、b、c、d的大小结果是（按从小到大的顺序排列）．

查看试题解析
12. 计算（﹣3x³）²=

查看试题解析
13.
如图，五边形ABCDE是一块草地．小明从点S出发，沿着这个五边形的边步行一周，最后仍回到起点S处，小明在各拐弯处转过的角度之和是

查看试题解析
14.
如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为

查看试题解析
15.
如图，a∥b，则∠A=

查看试题解析
16. 已知等腰三角形的两条边长分别是7和3，则此三角形的周长为．

查看试题解析
17.
如图，CD、CE分别是△ABC的高和角平分线，∠A=30°，∠B=60°，则∠DCE=

查看试题解析
18. 已知a、b、c为△ABC的三边，则化简|a+b+c|﹣|a﹣b﹣c|﹣|a﹣b+c|﹣|a+b﹣c|=

查看试题解析

三、解答题

19. 计算：
（1）（﹣a³）⁴•（﹣a²）⁵；
（2）（﹣a²）³﹣6a²•a⁴；
（3）3⁰﹣2﹣3+（﹣3）²﹣（﹣ $\frac{1}{4}$ ）^﹣1；
（4） ${(3 \frac{1}{8})}^{12} \times {(\frac{8}{25})}^{11} \times {(- 2)}^{3}$ ．

查看试题解析
20.
根据题意结合图形填空：已知：如图，AD⊥BC于D，EG⊥BC与G，∠E=∠3，试问：AD是∠BAC的平分线吗？若是，请说明理由．
答：是，理由如下：
∵AD⊥BC，EG⊥BC（已知）
∴∠4=∠5=90°（）
∴AD∥EG（）
∴∠1=∠E（）
∠2=∠3（）
∵∠E=∠3（已知）
∴（∠1）=（∠2）（等量代换）
∴AD是∠BAC的平分线（）

查看试题解析
21. （1）已知a^x=5，a^x+y=25，求a^x+a^y的值；
（2）已知10^α=5，10^β=6，求10^2α^﹣2β的值．

查看试题解析
22. 一个多边形的内角和加上它的外角和等于900°，求此多边形的边数．

查看试题解析
23.
如图，∠E=∠1，∠3+∠ABC=180°，BE是∠ABC的角平分线．你能判断DF与AB的位置关系吗？请说明理由．

查看试题解析
24.
如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．
（1）△ABC的面积；
（2）将△ABC经过平移后得到△A′B′C′，图中标出了点B的对应点B′，补全△A′B′C′；
（3）若连接AA′，BB′，则这两条线段之间的关系；
（4）在图中画出△ABC的高CD．

查看试题解析
25. 小丽在学习了“除零以外的任何数的零次幂的值为1”后，遇到这样一道题：“如果（x﹣2）^x+3=1，求x的值”，她解答出来的结果为x=﹣3．老师说她考虑的问题不够全面，你能帮助小丽解答这个问题吗？

查看试题解析
26.
如图1，MA₁∥NA₂ ，则∠A₁+∠A₂= 度．
如图2，MA₁∥NA₃ ，则∠A₁+∠A₂+∠A₃= 度．
如图3，MA₁∥NA₄ ，则∠A₁+∠A₂+∠A₃+∠A₄= 度．
如图4，MA₁∥NA₅ ，则∠A₁+∠A₂+∠A₃+∠A₄+∠A₅= 度．从上述结论中你发现了什么规律？
如图5，MA₁∥NA_n ，则∠A₁+∠A₂+∠A₃+…+∠A_n= 度．

查看试题解析
27. 观察下列等式，并回答有关问题：
$1^{3} + 2^{3} = \frac{1}{4} \times 2^{2} \times 3^{2}$ ；
$1^{3} + 2^{3} + 3^{3} = \frac{1}{4} \times 3^{2} \times 4^{2}$ ；
$1^{3} + 2^{3} + 3^{3} + 4^{3} = \frac{1}{4} \times 4^{2} \times 5^{2}$ ；
…
（1）若n为正整数，猜想1³+2³+3³+…+n³的值；
（2）利用上题的结论比较1³+2³+3³+…+100³与5000²的大小．

查看试题解析
28.
如图①，把△ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置．通过计算我们知道：2∠A=∠1+∠2．请你继续探索：
（1）如果把△ABC纸片沿DE折叠，使点A落在四边形BCED外部点A′的位置，如图②所示．此时∠A与∠1、∠2之间存在什么样的关系？并说明理由．
（2）如果把四边形ABCD沿EF折叠，使点A、D分别落在四边形BCFE内部点A′、D′的位置，如图③所示．你能求出∠A′、∠D′、∠1 与∠2之间的关系吗？并说明理由．

查看试题解析