广西南宁市2017年中考数学一模试卷
试卷更新日期:2017-11-07 类型:中考模拟
一、选择题
-
1. ﹣2的相反数是( )A、2 B、﹣2 C、 D、﹣2. 如图是一个圆柱体,则它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 我国是个缺水国家,目前可利用淡水资源总量仅约为899 000乙亿米3 , 其中数据899 000用科学记数法表示为( )A、8.99×104 B、0.899×106 C、899×103 D、8.99×1054. 下列运算正确的是( )A、6ab÷2a=3ab B、(2x2)3=6x6 C、a2•a5=a7 D、a8÷a2=a45. 平面直角坐标系内一点P(﹣2,3)关于原点对称的点的坐标是( )
3. 我国是个缺水国家,目前可利用淡水资源总量仅约为899 000乙亿米3 , 其中数据899 000用科学记数法表示为( )A、8.99×104 B、0.899×106 C、899×103 D、8.99×1054. 下列运算正确的是( )A、6ab÷2a=3ab B、(2x2)3=6x6 C、a2•a5=a7 D、a8÷a2=a45. 平面直角坐标系内一点P(﹣2,3)关于原点对称的点的坐标是( )
A、(3,﹣2) B、(2,﹣3) C、(﹣2,﹣3) D、(2,3)6. 不等式3(x﹣1)≤5﹣x的非负整数解有( )A、1个 B、2个 C、3个 D、4个7. 如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的大小是( ) A、20° B、35° C、130° D、140°8. 如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A、20° B、35° C、130° D、140°8. 如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( ) A、90° B、135° C、150° D、270°9. 小张抛掷两枚质地均匀的硬币,出现两枚硬币全部正面朝上的概率是( )
A、90° B、135° C、150° D、270°9. 小张抛掷两枚质地均匀的硬币,出现两枚硬币全部正面朝上的概率是( )
A、 B、 C、 D、110. 某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( ) A、50米 B、100米 C、125米 D、150米11. 在△ABC中,AB=3,BC=4,AC=2,D,E,F分别为AB,BC,AC中点,连接DF,FE,则四边形DBEF的周长是( )
A、50米 B、100米 C、125米 D、150米11. 在△ABC中,AB=3,BC=4,AC=2,D,E,F分别为AB,BC,AC中点,连接DF,FE,则四边形DBEF的周长是( ) A、5 B、7 C、9 D、1112. 如图,直线y=x+4与双曲线y=﹣ 相交于A、B两点,点P是y轴上的一个动点,当PA+PB的值最小时,点P的坐标为( )
A、5 B、7 C、9 D、1112. 如图,直线y=x+4与双曲线y=﹣ 相交于A、B两点,点P是y轴上的一个动点,当PA+PB的值最小时,点P的坐标为( )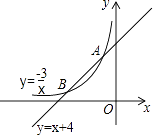 A、(0, ) B、(0, ) C、(0,﹣ ) D、(0,﹣ )
A、(0, ) B、(0, ) C、(0,﹣ ) D、(0,﹣ )二、填空题
-
13. 使 有意义的x的取值范围是 .14. 某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下:52,60,62,54,58,62.这组数据的中位数是 .15. 单项式﹣ 的系数是 , 次数是 .16. 如图,点A为反比例函数y= 图象上的一点,过点作AB⊥x轴于点B,连接OA,若△OAB的面积为4,则k= .
 17. 如图,在△ABC中,∠BAC=50°,AC=2,AB=3.现将△ABC绕A点逆时旋转50°得到△AB1C1 , 则图中的阴影部分的面积为 .
17. 如图,在△ABC中,∠BAC=50°,AC=2,AB=3.现将△ABC绕A点逆时旋转50°得到△AB1C1 , 则图中的阴影部分的面积为 . 18. 如图,小强作出边长为1的第1个等边△A1B1C1 , 计算器面积为S1 , 然后分别取△A1B1C1三边的中点A2、B2、C1 , 作出第2个等边△A2B2C2 , 计算其面积为S2 , 用同样的方法,作出第3个等边△A3B3C3 , 计算其面积为S3 , 按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20= .
18. 如图,小强作出边长为1的第1个等边△A1B1C1 , 计算器面积为S1 , 然后分别取△A1B1C1三边的中点A2、B2、C1 , 作出第2个等边△A2B2C2 , 计算其面积为S2 , 用同样的方法,作出第3个等边△A3B3C3 , 计算其面积为S3 , 按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20= .
三、解答题
-
19. 计算:﹣12+6sin60°﹣ +20170 .20. 先化简,再求值:(3﹣x)(3+x)+(x+1)2 , 其中x=2.21. 如图,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点顺时针方向旋转180°后得到四边形A1B1C1D1 .
 (1)、写出点D1的坐标;(2)、将四边形A1B1C1D1平移,得到四边形A2B2C2D2 , 若点D2(4,5),画出平移后的图形;(3)、求点D旋转到点D1所经过的路线长.22. 如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
(1)、写出点D1的坐标;(2)、将四边形A1B1C1D1平移,得到四边形A2B2C2D2 , 若点D2(4,5),画出平移后的图形;(3)、求点D旋转到点D1所经过的路线长.22. 如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF. (1)、证明:△BEO≌△DFO;(2)、证明:四边形ABCD是平行四边形.23. 某校为了解本校中考体育备考情况,随机抽去九年级部分学生进行了一次测试(满分60分,成绩均记为整数分)并按测试成绩(单位:分)分成四类:A类(54≤a≤60),B类(48≤a≤53),C类(36≤a≤47),D类(a≤35)绘制出如下两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)、证明:△BEO≌△DFO;(2)、证明:四边形ABCD是平行四边形.23. 某校为了解本校中考体育备考情况,随机抽去九年级部分学生进行了一次测试(满分60分,成绩均记为整数分)并按测试成绩(单位:分)分成四类:A类(54≤a≤60),B类(48≤a≤53),C类(36≤a≤47),D类(a≤35)绘制出如下两幅不完整的统计图,请根据图中信息,解答下列问题: (1)、请补全统计图;(2)、在扇形统计图汇总,表示成绩类别为“C”的扇形所对应的圆心角是度;(3)、该校准备召开体育考经验交流会,已知A类学生中有4人满分(男生女生各有2人),现计划从这4人中随机选出2名学生进行经验介绍,请用树状图或列表法求所抽到的2,名学生恰好是一男一女的概率24. 某校为了创建书香校园,今年又购进一批图书,经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等.
(1)、请补全统计图;(2)、在扇形统计图汇总,表示成绩类别为“C”的扇形所对应的圆心角是度;(3)、该校准备召开体育考经验交流会,已知A类学生中有4人满分(男生女生各有2人),现计划从这4人中随机选出2名学生进行经验介绍,请用树状图或列表法求所抽到的2,名学生恰好是一男一女的概率24. 某校为了创建书香校园,今年又购进一批图书,经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等.
(1)、今年购进的文学书和科普书的单价各是多少元?(2)、该校购买这两种书共180本,总费用不超过2000元,且购买文学书的数量不多于42本,应选择哪种购买方案可使总费用最低?最低费用是多少元?