2015-2016学年江苏省无锡市宜兴市和桥二中七年级下学期第一次月考数学试卷
试卷更新日期:2016-08-08 类型:月考试卷
一、单选题
-
1. 下列长度的3条线段,能构成三角形的是( )A、1,2,3 B、2,3,4 C、6,6,12 D、5,6,12
-
2. 下列运算正确的是( )A、a+a2=2a3 B、a2•a3=a6 C、(a2)3=a5 D、a6÷a3=a3
-
3. [﹣(﹣a)2]3=( )A、﹣a6 B、a6 C、- D、
-
4. 下列各式计算结果为a7的是( )A、(﹣a)2•(﹣a)5 B、(﹣a)2•(﹣a5) C、(﹣a2)•(﹣a)5 D、(﹣a)•(﹣a)6
-
5. 若a= , b= , c=0.8﹣1 , 则a、b、c三数的大小关系是( )A、a<b<c B、a>b>c C、a>c>b D、c>a>b
-
6. 下列说法中错误的是( )A、任意三角形的内角和都是180° B、三角形按边分可分为不等边三角形和等腰三角形 C、三角形的中线、角平分线、高都是线段 D、三角形的一个外角大于任何一个内角
-
7. 在下列各图的△ABC中,正确画出AC边上的高的图形是( )A、
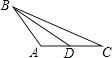 B、
B、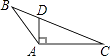 C、
C、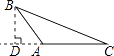 D、
D、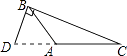
-
8.
如图,下列条件中:
(1)∠B+∠BCD=180°;
(2)∠1=∠2;
(3)∠3=∠4;
(4)∠B=∠5.
能判定AB∥CD的条件个数有( )
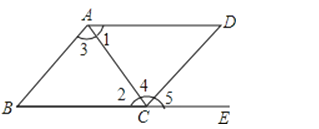 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
9.
如图,AB∥CD,E是BD上的一点.下列结论中,正确的是( )
 A、∠1=∠2﹣∠3 B、∠2=∠1﹣∠3 C、∠3=∠1+∠2 D、∠1+∠2+∠3=180°
A、∠1=∠2﹣∠3 B、∠2=∠1﹣∠3 C、∠3=∠1+∠2 D、∠1+∠2+∠3=180° -
10.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , …按此规律,要使得到的三角形的面积超过2010,最少经过( )次操作.
 A、6 B、5 C、4 D、3
A、6 B、5 C、4 D、3
二、填空题
-
11. PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为 .
-
12. 计算:
a6÷a2=
(﹣2ab2)2=
42005×0.252006=
-
13. 已知10x=2,10y=3,则10x﹣y=
-
14.
将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是

-
15. 一个等腰三角形的边长分别是4cm和7cm,则它的周长是
-
16.
如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是

-
17.
如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2= 度.

-
18.
如图①,点E、F分别为长方形纸带ABCD的边AD、BC上的点,∠DEF=19°,将纸带沿EF折叠成图②(G为ED和EF的交点,再沿BF折叠成图③(H为EF和DG的交点),则图③中∠DHF=

三、解答题
-
19. 计算:
(1)
(2)(p﹣q)4÷(q﹣p)3•(p﹣q)2
(3)a•a2•a3+(﹣2a3)2﹣a8÷a2
(4)(﹣2x)2•(x2)3÷(﹣x)2 .
-
20. (1)已知am=2,an=3,求①am+n的值;②a3m﹣2n的值
(2)已知2×8x×16=223 , 求x的值.
-
21.
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)补全△A′B′C′根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积

-
22. 一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.
-
23.
如图,在△ABC中,∠B=24°,∠ACB=104°,AD⊥BC于D,AE平分∠BAC,求∠DAE的度数.

-
24.
如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.

试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2()
∠1=∠3()
∴∠2=∠3()
∴∥()
∴∠C=∠ABD ()
又∵∠C=∠D()
∴∠D=∠ABD()
∴AC∥DF()
-
25.
实验探究:
(1)动手操作:
①如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD=
②如图2,若直角三角板ABC不动,改变等腰直角三角板DEF的位置,使三角板DEF的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD=

(2)猜想证明:
如图3,∠BDC与∠A、∠B、∠C之间存在着 关系
(3)灵活应用:
请你直接利用以上结论,解决以下列问题:
①如图4,BE平分∠ABD,CE平分∠ACB,若∠BAC=40°,∠BDC=120°,∠BEC
②如图5,∠ABD,∠ACD的10等分线相交于点F1、F2、…、F9 ,
若∠BDC=120°,∠BF3C=64°,则∠A的度数为
-
26.
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=35°,求∠ACB的度数;
②若∠ACB=150°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)请你动手操作,现将三角尺ACD固定,三角尺BCE的CE边与CA边重合,绕点C顺时针方向旋转,当0°<∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

