浙江省湖州市2017年中考数学模拟试卷
试卷更新日期：2017-11-07 类型：中考模拟
一、选择题
-
1. ﹣5的相反数是（ ）A、 B、 C、﹣5 D、52. 计算（﹣a3）2的结果是（ ）A、a5 B、﹣a5 C、a6 D、﹣a63. 若函数y=kx的图象经过点（﹣1，2），则k的值是（ ）A、﹣2 B、2 C、﹣ D、4. 如图，直线a∥b，直线c分别与a，b相交，∠1=50°，则∠2的度数为（ ）
A、150° B、130° C、100° D、50°5. 以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是（ ）A、
B、
C、
D、
6. 如图，点A为反比例函数y=﹣ 图象上一点，过点A作AB⊥x轴于点B，连结OA，则△ABO的面积为（ ）
A、16 B、8 C、4 D、27. 如图，⊙O与AB相切于点A，BO与⊙O交于点C，∠BAC=30°，则∠B等于（ ）
A、20° B、30° C、50° D、60°8. 一个不透明布袋中有红球10个，白球2个，黑球x个，每个球除颜色外都相同，从中任取一个球，取得的球是红球的概率是 ，则x的值为（ ）A、5 B、4 C、3 D、29. 如图，在△ABC中，AC=4，BC=2，点D是边AB上一点，CD将△ABC分成△ACD和△BCD，若△ACD是以AC为底的等腰三角形，且△BCD与△BAC相似，则CD的长为（ ）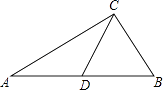
A、 B、2 C、4 ﹣4 D、10. 如图1，在Rt△ABC中，∠A=90°，BC=10cm，点P、点Q同时从点B出发，点P以2cm/s的速度沿B→A→C运动，终点为C，点Q以1cm/s的速度沿B→C运动，当点P到达终点时两个点同时停止运动，设点P，Q出发t秒时，△BPQ的面积为ycm2 ， 已知y与t的函数关系的图象如图2（曲线OM和MN均为抛物线的一部分），给出以下结论：①AC=6cm；②曲线MN的解析式为y=﹣ t2+ t（4≤t≤7）；③线段PQ的长度的最大值为 ；④若△PQC与△ABC相似，则t= 秒．其中正确的是（ ）
A、①②④ B、②③④ C、①③④ D、①②③二、填空题
-
11. 分解因式：x2﹣16= ．12. 不等式组 的解集是 ．13. 一个小球由地面沿着坡度1：2的坡面向上前进了10米，此时小球距离地面的高度为米．14. 已知一组数据a1 ， a2 ， a3 ， a4的平均数是2017，则另一组数据a1+3，a2﹣2，a3﹣2，a4+5的平均数是 ．15. 已知二次函数y=（x﹣h）2+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为 ．16. 如图，在矩形ABCD中，AB=3，BC=2，点F是BC的中点，点E是边AB上一点，且BE=2，连结DE，EF，并以DE，EF为边作▱EFGD，连结BG，分别交EF和DC于点M，N，则 = ．
三、解答题
-
17. 计算：24÷（﹣2）3﹣3．18. 解方程： = ．19. 如图，已知在△ABC中，点D，E，F分别在BC，AB，AC边上．
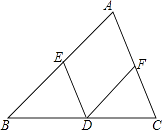(1)、当点D，E，F分别为BC，AB，AC边的中点时，求证：△BED≌△DFC；(2)、若DE∥AC，DF∥AB，且AE=2，BE=3，求 的值．20. 3月5日是学雷锋日，某校组织了以“向雷锋同志学习”为主题的小报制作比赛，评分结果只有60，70，80，90，100五种．现从中随机抽取部分作品，对其份数及成绩进行整理，制成如下两幅不完整的统计图．根据以下信息，解答下列问题：
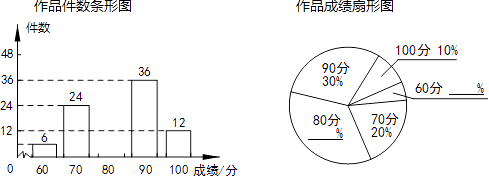(1)、求本次抽取了多少份作品，并补全两幅统计图；(2)、已知该校收到参赛作品共1200份，请估计该校学生比赛成绩达到90分以上（含90分）的作品有多少份？21. 如图，AB是⊙O的直径，AE平分∠BAF，交⊙O于点E，过点E作直线ED⊥AF，交AF的延长线于点D，交AB的延长线于点C．
(1)、求证：CD是⊙O的切线；(2)、若tanC= ，⊙O的半径为2，求DE的长．22. 为更新果树品种，某果园计划新购进A，B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种树苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．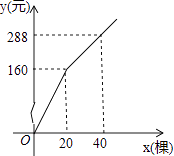
(1)、求y与x的函数关系式；(2)、若在购买计划中，B种树苗的数量不超过35棵，但不少于A种树苗的数量，请设计购买方案，使总费用最低，并求出最低费用．23. 综合题
(1)、【问题提出】如图1．△ABC是等边三角形，点D在线段AB上．点E在直线BC上．且∠DEC=∠DCE．求证：BE=AD；
(2)、【类比学习】如图2．将条件“点D在线段AB上”改为“点D在线段AB的延长线上”，其他条件不变．判断线段AB，BE，BD之间的数量关系，并说明理由．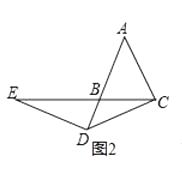
(3)、【扩展探究】如图3．△ABC是等腰三角形，AB=AC，∠BAC=120°，点D在线段AB的反向延长线上，点E在直线BC上，且∠DEC=∠DCE，【类比学习】中的线段AB、BE、BD之间的数量关系是否还成立？若成立，请说明理由；若不成立，请直接写出线段AB，BE，BD之间的数量．
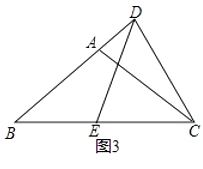24. 如图，抛物线y=ax2+ x+1（a≠0）与x轴交于A，B两点，其中点B坐标为（2，0）．
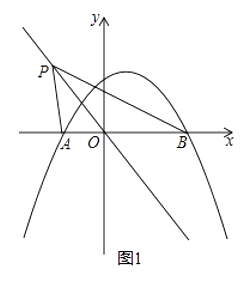(1)、求抛物线的解析式和点A的坐标；(2)、如图1，点P是直线y=﹣x上的动点，当直线OP平分∠APB时，求点P的坐标；(3)、如图2，在（2）的条件下，点C是直线BP上方的抛物线上的一个动点，过点C作y轴的平行线，交直线BP于点D，点E在直线BP上，连结CE，以CD为腰的等腰△CDE的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．