2015-2016学年山东省济宁市微山县八年级下学期期中数学试卷

试卷更新日期：2016-08-05 类型：期中考试

进入出卷网下载

一、单选题

1. 若式子 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（　　）

A、x≥1 B、x＞1 C、x＜1 D、x≤1

查看试题解析
2.
如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是（　　）

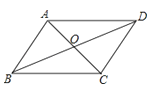A、AB∥CD B、AB=CD C、AC=BD D、OA=OC

查看试题解析
3. 在一次夏令营活动中，小霞同学从营地A点出发，要到距离A点10千米的C地去，先沿北偏东70°方向走了8千米到达B地，然后再从B地走了6千米到达目的地C，此时小霞在B地的（）

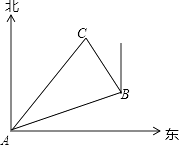A、北偏东20°方向上 B、北偏西20°方向上 C、北偏西30°方向上 D、北偏西40°方向上

查看试题解析
4. 若直角三角形的两边长分别为a，b，且满足 $\sqrt{a^{2} - 6 a + 9}$ +|b﹣4|=0，则该直角三角形的第三边长为（　　）

A、5 B、 $\sqrt{7}$ C、4 D、5或 $\sqrt{7}$

查看试题解析
5. 下列运算正确的是（　　）

A、 $\sqrt{8}$ - $\sqrt{2}$ = $\sqrt{2}$ B、 $\sqrt{4 \frac{1}{9}} = 2 \frac{1}{3}$ C、 $\sqrt{5}$ - $\sqrt{3}$ = $\sqrt{2}$ D、 $\sqrt{{(2 - \sqrt{5})}^{2}} = 2 - \sqrt{5}$

查看试题解析
6.
如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是（　　）

A、BC=AC B、CF⊥BF C、BD=DF D、AC=BF

查看试题解析
7. 如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为（）

A、6 B、8 C、10 D、12

查看试题解析
8. 如图，已知矩形ABCD中，R，P分别是DC、BC上的点，E，F分别是AP，RP的中点，当P在BC上从B向C移动而R不动时，那么下列结论成立的是（）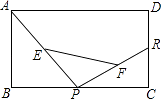

A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不改变 D、线段EF的长不能确定

查看试题解析
9. 如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD，若AC=2，∠ADC=30°，
①四边形ACED是平行四边形；
②△BCE是等腰三角形；
③四边形ACEB的周长是10+2 $\sqrt{13}$ ；
④四边形ACEB的面积是16．
则以上结论正确的是（）

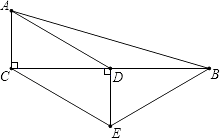A、①②③ B、①②④ C、①③④ D、②④

查看试题解析

二、填空题

10. 已知直角三角形的两条直角边长为6，8，那么斜边上的中线长是

查看试题解析
11. 已知最简二次根式 $\sqrt{7 - 2 a}$ 与2 $\sqrt{3}$ 可以合并，则a的值是

查看试题解析
12.
如图所示，矩形ABCD的两条对角线相交于点O，∠AOB=60°，AB=2，则矩形的对角线AC的长是

查看试题解析
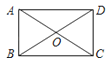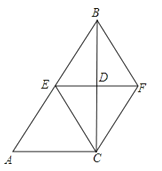
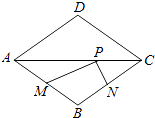
13.
如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则PM+PN的最小值是．

查看试题解析
14. 观察下列勾股数
第一组：3=2×1+1，4=2×1×（1+1），5=2×1×（1+1）+1
第二组：5=2×2+1，12=2×2×（2+1），13=2×2×（2+1）+1
第三组：7=2×3+1，24=2×3×（3+1），25=2×3×（3+1）+1
第四组：9=2×4+1，40=2×4×（4+1），41=2×4×（4+1）+1
…观察以上各组勾股数组成特点，第7组勾股数是（只填数，不填等式）

查看试题解析

三、计算题

15. 计算：

（1）2 $\sqrt{12}$ ﹣6 $\sqrt{\frac{1}{3}}$ +3 $\sqrt{48}$

（2）（ $\sqrt{6}$ ﹣ $\sqrt{5}$ ）（ $\sqrt{6}$ + $\sqrt{5}$ ）+（2 $\sqrt{3}$ ﹣3 $\sqrt{2}$ ）² ．

查看试题解析

四、解答题

16.
如图，四边形ABCD中，AD∥BC，AE⊥AD交BD于点E，CF⊥BC交BD于点F，且AE=CF．求证：四边形ABCD是平行四边形．

查看试题解析
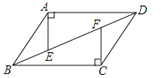17.
如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，分别按下列要求画以格点为顶点三角形和平行四边形．
（1）三角形三边长为4，3 $\sqrt{2}$ ， $\sqrt{10}$ ；
（2）平行四边形有一锐角为45°，且面积为6．

查看试题解析
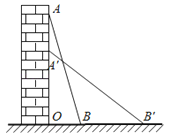
18.
一架方梯AB长25米，如图所示，斜靠在一面上：
（1）若梯子底端离墙7米，这个梯子的顶端距地面有多高？
（2）在（1）的条件下，如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？

查看试题解析
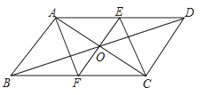
19.
如图：在平行四边形ABCD中，对角线AC与BD交于点O，过点O的直线EF分别与AD、BC交于点E、F，EF⊥AC，连结AF、CE．
（1）求证：OE=OF；
（2）请判断四边形AECF是什么特殊四边形，请证明你的结论．

查看试题解析
20. 观察下列各式：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}}$ =1+ $\frac{1}{1}$ ﹣ $\frac{1}{2}$ =1 $\frac{1}{2}$
$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}}$ =1+ $\frac{1}{2}$ ﹣ $\frac{1}{3}$ =1 $\frac{1}{6}$
$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}}$ =1+ $\frac{1}{3}$ ﹣ $\frac{1}{4}$ =1 $\frac{1}{12}$
请你根据上面三个等式提供的信息，猜想：

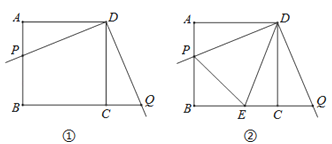
(1)、 $\sqrt{1 + \frac{1}{4^{2}} + \frac{1}{5^{2}}}$ =

(2)、请你按照上面每个等式反映的规律，写出用n（n为正整数）表示的等式：

(3)、利用上述规律计算： $\sqrt{\frac{50}{49} + \frac{1}{64}}$ （仿照上式写出过程）

查看试题解析
21.
某校数学兴趣小组开展了一次课外活动，过程如下：如图①，正方形ABCD中，AB=4，将三角板放在正方形ABCD上，使三角板的直角顶点与D点重合．三角板的一边交AB于点P，另一边交BC的延长线于点Q．
（1）求证：AP=CQ；
（2）如图②，小明在图1的基础上作∠PDQ的平分线DE交BC于点E，连接PE，他发现PE和QE存在一定的数量关系，请猜测他的结论并予以证明；
（3）在（2）的条件下，若AP=1，求PE的长．

查看试题解析