陕西省西安市雁塔区电子科大附中2017年中考数学八模试卷
试卷更新日期：2017-11-06 类型：中考模拟
一、选择题
-
1. ﹣ 的相反数是（ ）A、 B、﹣ C、3 D、﹣32. 如图是一个零件的立体图，该零件的俯视图是（ ）
A、
B、
C、
D、
3. 下列计算错误的是（ ）A、a•a=a2 B、2a+a=3a C、（a3）2=a5 D、a3÷a﹣1=a44. 如图，已知AB∥CD，BC平分∠ABE，∠C=33°，则∠BED的度数是（ ）
A、16° B、33° C、49° D、66°5. 若一次函数y=kx+b的图象经过点P（﹣2，3），则2k﹣b的值为（ ）
A、2 B、﹣2 C、3 D、﹣36. 不等式组 的整数解的个数为（ ）
A、6 B、7 C、8 D、97. 如图，G是正方形形ABCD的边BC上一点，DE、BF分别垂直AG于点E、F，则图中与△ABF相似的三角形有（ ）
A、1个 B、2个 C、3个 D、4个8. 如图，把直线y=2x向下平移后得到直线AB，直线AB与x轴、y轴分别相交于点A，B．若△ABO的面积是1，则直线AB的解析式是（ ）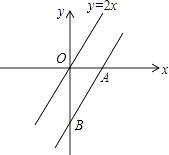
A、y=3x+ B、y=2x﹣ C、y=3x﹣2 D、y=2x﹣29. 如图，已知△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则BC的长为（ ）
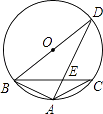A、 B、6 C、 D、10. 若二次函数y=ax2+bx+c（a＜0）的图象如图所示，且关于x的方程ax2+bx+c=k有两个不相等的实根，则常数k的取值范围是（ ）
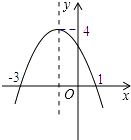A、0＜k＜4 B、﹣3＜k＜1 C、k＜﹣3或k＞1 D、k＜4二、填空题
-
11. 分解因式：x2y﹣4y=12. 请从以下两个小题中任选一个作答，若多选，则按第一题计分．
A．一个多边形的每个内角都等于150°，则这个多边形是边形．
B．用计算器计算：sin15°32'（精确到0.01）
13. 如图，已知双曲线 经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣6，4），则△AOC的面积为 ．
14. 如图，在Rt△ABC中，∠ACB=90°，AC=BC，点M在AC边上，且AM=2，MC=6，动点P在AB边上，连接PC，PM，则PC+PM的最小值是 ．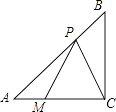
三、解答题
-
15. 计算：（ ）﹣1+|﹣ |﹣（π﹣3）0+3tan30°．16. 先化简，再求值： ÷（1﹣ ），其中a=﹣ ．
17. 如图，已知△ABC，AB＜BC，请用尺规作图的方法在BC上取一点P，使得PA+PC=BC（保留作图痕迹，不写作法）
18. 中考体育测试前，某区教育局为了了解选报引体向上的初三男生的成绩情况，随机抽测了本区部分选报引体向上项目的初三男生的成绩，并将测试得到的成绩绘成了下面两幅不完整的统计图：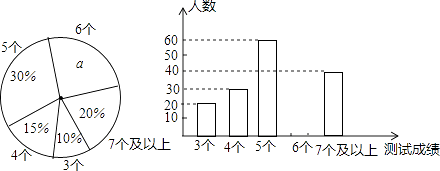
请你根据图中的信息，解答下列问题：
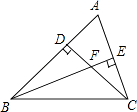
(1)、写出扇形图中a=%，并补全条形图；(2)、在这次抽测中，测试成绩的众数和中位数分别是 个、个．(3)、该区体育中考选报引体向上的男生共有1800人，如果体育中考引体向上达6个以上（含6个）得满分，请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名？19. 已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点F．求证：BF=AC．
20. 小明想用镜子测量一棵松树的高度，但因树旁有一条河，不能测量镜子与树之间的距离，于是他两次利用镜子，如图所示，第一次他把镜子放在C点，人在F点时正好在镜子中看到树尖A；第二次把镜子放在D点，人在G点正好看到树尖A．已知小明的眼睛距离地面1.70m，量得CD=12m，CF=1.8m，DH=3.8m．请你求出松树的高．
21. 某学校期末考试要给学生印制复习资料若干份，印刷厂有甲、乙两种收费方式，除按印刷份数收取印刷费用外，甲种方式还收取制版费，而乙种不需要，两种印刷方式的费用y（元）与印刷份数x（份）之间的函数关系如图所示：
(1)、填空：甲种收费方式的函数关系式是 ， 乙种收费方式的函数关系式是 ．(2)、若需印刷100﹣400份（含100和400）份复习资料，选择哪种印刷方式比较合算．22. 小晗家客厅里装有一种三位单极开关，分别控制着A（楼梯）、B（客厅）、C（走廊）三盏电灯，在正常情况下，小晗按下任意一个开关均可打开对应的一盏电灯，既可三盏、两盏齐开，也可分别单盏开．因刚搬进新房不久，不熟悉情况．
(1)、若小晗任意按下一个开关，正好楼梯灯亮的概率是多少？
(2)、若任意按下一个开关后，再按下另两个开关中的一个，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图法或列表法加以说明．
23. 如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．
(1)、求证：DE为⊙O的切线；
(2)、若⊙O的半径为5，∠BAC=60°，求DE的长．
24. 如图，抛物线y= x2+bx+c经过A（﹣1，0），C（2，﹣3）两点，与y轴交于点D，与x轴交于另一点B．
(1)、求此抛物线的解析式及顶点坐标；(2)、若将此抛物线平移，使其顶点为点D，需如何平移？写出平移后抛物线的解析式；(3)、过点P（m，0）作x轴的垂线（1≤m≤2），分别交平移前后的抛物线于点E，F，交直线OC于点G，求证：PF=EG．25. 综合题，如图，正方形ABCD。(1)、请在图①中作两条直线，使它们将正方形ABCD的面积三等分；
(2)、如图②，在矩形ABCD中，AB=6，BC=9，在图②中过顶点A作两条直线，使它们将矩形ABCD的面积三等分，井说明理由；
(3)、如图③，农博园有一块不规则的五边形ABCDE空地，其中AB∥CD、AE∥BC，AB=AC=100米，AE=160米，BC=120米，CD=62.5米，根据视觉效果和花期特点，农博园设计部门想在这片空地种上等面积的三种不同的花，要求从入口A点处修两条笔直的小路（小路的面积忽略不计）方便游客赏花，两条小路将这块地面积三等分．请通过计算画图说明其设计部们能否实现，若能实现请确定小路尽头的位置．