辽宁省丹东七中2017年中考数学二模试卷
试卷更新日期:2017-11-06 类型:中考模拟
一、选择题
-
1. ﹣ 的倒数是( )A、﹣4 B、4 C、 D、﹣2. 下列计算正确的是( )A、2a3+a2=3a5 B、(3a)2=6a2 C、(a+b)2=a2+b2 D、2a2•a3=2a53. 如图所示的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是( )
4. 如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是( ) A、
A、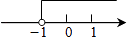 B、
B、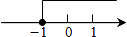 C、
C、 D、
D、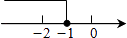 5. 如图是某射击选手5次射击成绩的折线图,根据图示信息,这5次成绩的众数、中位数分别是( )
5. 如图是某射击选手5次射击成绩的折线图,根据图示信息,这5次成绩的众数、中位数分别是( ) A、7、9 B、7、8 C、8、9 D、8、106. 如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
A、7、9 B、7、8 C、8、9 D、8、106. 如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( ) A、1 B、2 C、3 D、47. 如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y= (x>0)的图象上,已知点B的坐标是( , ),则k的值为( )
A、1 B、2 C、3 D、47. 如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y= (x>0)的图象上,已知点B的坐标是( , ),则k的值为( ) A、4 B、6 C、8 D、108. 如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
A、4 B、6 C、8 D、108. 如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
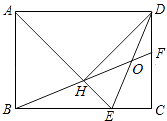 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 目前发现一种病毒直径约是0.0000252米,将0.0000252用科学记数法表示为 .10. 若关于x的一元二次方程kx2+4x+3=0有实数根,则k的取值范围是 .11. 如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=度.
 12. 在△ABC中,∠B=45°,cosA= ,则∠C的度数是 .13. 关于x,y的方程组 的解是 ,则|m+n|的值是 .14. 如图,在平行四边形ABCD中,E为CD上一点,DE:EC=2:3,连接AE,BE,BD,且AE,BD交于点F,则S△DEF:S△EBF:S△ABF= .
12. 在△ABC中,∠B=45°,cosA= ,则∠C的度数是 .13. 关于x,y的方程组 的解是 ,则|m+n|的值是 .14. 如图,在平行四边形ABCD中,E为CD上一点,DE:EC=2:3,连接AE,BE,BD,且AE,BD交于点F,则S△DEF:S△EBF:S△ABF= . 15. 如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1 , AA2 , AA3…,依此作法,则∠AAnAn+1等于度.(用含n的代数式表示,n为正整数)
15. 如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1 , AA2 , AA3…,依此作法,则∠AAnAn+1等于度.(用含n的代数式表示,n为正整数)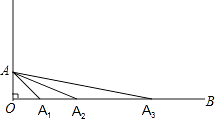
三、解答题
-
16. 先化简,再求值:( ﹣ )÷ ,其中x=( )﹣1﹣(π﹣1)0+ .
17. 如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2). (1)、请画出△ABC关于y轴对称的△A1B1C1;(2)、以原点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2 , 画出△A2B2C2 , 并直接写出S :S = .
(1)、请画出△ABC关于y轴对称的△A1B1C1;(2)、以原点O为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2 , 画出△A2B2C2 , 并直接写出S :S = .四、综合题
-
18. 某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为A、B、C、D四个等级,绘制了图①、图②两幅不完整的统计图,请结合图中所给信息解答下列问题:
 (1)、求本次被抽查的学生共有多少人?(2)、将条形统计图和扇形统计图补充完整;(3)、求扇形统计图中“A”所在扇形圆心角的度数;(4)、估计全校“D”等级的学生有多少人?19. 有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.(1)、请画出树状图并写出(m,n)所有可能的结果;(2)、求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
(1)、求本次被抽查的学生共有多少人?(2)、将条形统计图和扇形统计图补充完整;(3)、求扇形统计图中“A”所在扇形圆心角的度数;(4)、估计全校“D”等级的学生有多少人?19. 有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.(1)、请画出树状图并写出(m,n)所有可能的结果;(2)、求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
20. 晨光文具店用进货款1620元购进A品牌的文具盒40个,B品牌的文具盒60个,其中A品牌文具盒的进货单价比B品牌文具盒的进货单价多3元.(1)、求A、B两种文具盒的进货单价?(2)、已知A品牌文具盒的售价为23元/个,若使这批文具盒全部售完后利润不低于500元,B品牌文具盒的销售单价最少是多少元?21. 某海域有A,B,C三艘船正在捕鱼作业,C船突然出现故障,向A,B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向. (1)、求∠ABC的度数;
(1)、求∠ABC的度数;
(2)、A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).(参考数据: ≈1.414, ≈1.732)
22. 如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD. (1)、求证:CD是⊙O的切线;(2)、若AB=4,求图中阴影部分的面积.23. 国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A,B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同,销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系式yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系式yB=﹣x+14.
(1)、求证:CD是⊙O的切线;(2)、若AB=4,求图中阴影部分的面积.23. 国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A,B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同,销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系式yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系式yB=﹣x+14.
(1)、求A、B两种型号的汽车的进货单价;(2)、已知A型汽车的售价比B型汽车的售价高2万元/台,设B型汽车售价为t万元/台.每周销售这两种车的总利润为W万元,求W与t的函数关系式,A、B两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元?24. 如图①,点P是正方形ABCD的BC边上的一点,以DP为边长的正方形DEFP与正方形ABCD在BC的同侧,连接AC,FB.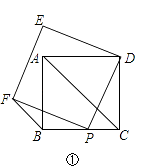 (1)、请你判断FB与AC又怎样的位置关系?并证明你的结论;(2)、若点P在射线CB上运动时,如图②,判断(1)中的结论FB与AC的位置关系是否仍然成立?并说明理由;
(1)、请你判断FB与AC又怎样的位置关系?并证明你的结论;(2)、若点P在射线CB上运动时,如图②,判断(1)中的结论FB与AC的位置关系是否仍然成立?并说明理由; (3)、当点P在射线CB上运动时,请你指出点E的运动路线,不必说明理由.25. 如图,直线y=﹣ x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
(3)、当点P在射线CB上运动时,请你指出点E的运动路线,不必说明理由.25. 如图,直线y=﹣ x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点. (1)、求抛物线的解析式;(2)、点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的 倍.
(1)、求抛物线的解析式;(2)、点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的 倍.①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)、点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.