江苏省苏州市2017学中考数学三模试卷

试卷更新日期：2017-11-06 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\frac{1}{3}$ 的倒数是（）

A、﹣ $\frac{1}{3}$ B、 $\frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 下列运算正确的是（）

A、a²+a⁵=a⁷ B、（﹣a²）³=a⁶ C、a²﹣1=（a+1）（a﹣1） D、（a+b）²=a²+b²

查看试题解析
3. 下列图形中，中心对称图形有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 有一种细胞直径约为0.000 058cm．用科学记数法表示这个数为（）

A、5.8×10^﹣⁶ B、5.8×10^﹣⁵ C、0.58×10^﹣⁵ D、58×10^﹣⁶

查看试题解析
5. 在“我为震灾献爱心”的捐赠活动中，某班40位同学捐款金额统计如下：
金额（元）
20
30
35
50
100
学生数（人）
3
7
5
15
10
则在这次活动中，该班同学捐款金额的众数和中位数是（）

A、30，35 B、50，35 C、50，50 D、15，50

查看试题解析
6. 使 $\sqrt{3 x - 1}$ 有意义的x的取值范围是（）

A、 $x > \frac{1}{3}$ B、 $x > - \frac{1}{3}$ C、 $x \geq \frac{1}{3}$ D、 $x \geq - \frac{1}{3}$

查看试题解析
7. 如图，l₁∥l₂∥l₃ ，直线a，b与l₁、l₂、l₃分别相交于A，B，C和点D，E，F．若 $\frac{A B}{B C}$ = $\frac{2}{3}$ ，DE=4，则EF的长是（）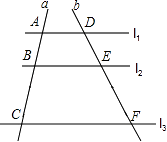

A、 $\frac{8}{3}$ B、 $\frac{20}{3}$ C、6 D、10

查看试题解析
8. 下列命题正确的是（）

A、两个等边三角形全等 B、各有一个角是40°的两个等腰三角形全等 C、对角线互相垂直平分的四边形是菱形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
9. 如图是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，则这个几何体的左视图为（）

A、 B、 C、 D、

查看试题解析
10. 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，点P以每秒一个单位的速度沿着B﹣C﹣A运动，⊙P始终与AB相切，设点P运动的时间为t，⊙P的面积为y，则y与t之间的函数关系图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 2^﹣¹等于．

查看试题解析
12. 分解因式：2a²﹣8= ．

查看试题解析
13. “五一”期间，某服装商店举行促销活动，全部商品八折销售，小华购买一件原价为140元的运动服，打折后他比按原价购买节省了元．

查看试题解析
14. 某校对学生上学方式进行了一次抽样调查，并根据此次调查结果绘制了一个不完整的扇形统计图，其中“其他”部分所对应的圆心角是36°，则“步行”部分所占百分比是．

查看试题解析
15. 如图，圆锥的底面半径为3cm，高为4cm，那么这个圆锥的侧面积是cm² ．

查看试题解析
16. 如图，若干全等正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需个五边形．

查看试题解析
17. 如图，在△ABC中，AB=5，AC=3，AD，AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连结DH，则线段DH的长为．

查看试题解析
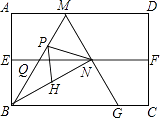
18. 如图，四边形ABCD是矩形纸片，AB=2．对折矩形纸片ABCD，使AD与BC重合，折痕为EF；展平后再过点B折叠矩形纸片，使点A落在EF上的点N，折痕BM与EF相交于点Q；再次展平，连接BN，MN，延长MN交BC于点G．有如下结论：
①∠ABN=60°；②AM=1；③QN= $\frac{\sqrt{3}}{3}$ ；④△BMG是等边三角形；⑤P为线段BM上一动点，H是BN的中点，则PN+PH的最小值是 $\sqrt{3}$ ．
其中正确结论的序号是．

查看试题解析

三、解答题

19. 计算：（ $\frac{1}{2}$ ）^﹣²﹣（π﹣ $\sqrt{7}$ ）⁰+| $\sqrt{3}$ ﹣2|+4sin60°．

查看试题解析
20. 解不等式组 ${\begin{matrix} 4 (x + 1) \leq 7 x + 10 \\ x - 5 < \frac{x - 8}{3} . \end{matrix}$ ．

查看试题解析
21. 先化简（ $\frac{1}{x - 2}$ ﹣ $\frac{2}{x}$ ）• $\frac{x^{2} - 2 x}{2}$ ，再从0，1，2中选一个合适的x的值代入求值．

查看试题解析
22. 为解决“最后一公里”的交通接驳问题，某市投放了大量公租自行车使用，到2014年底，全市已有公租自行车25000辆，租赁点600个，预计到2016年底，全市将有公租自行车50000辆，并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍，预计到2016年底，全市将有租赁点多少个？

查看试题解析
23. 关于x的一元二次方程x²+2x+k+1=0的实数解是x₁和x₂ ．

(1)、求k的取值范围；

(2)、如果x₁+x₂﹣x₁x₂＜﹣1且k为整数，求k的值．

查看试题解析
24. A，B，C三人玩篮球传球游戏，游戏规则是：第一次传球由A将球随机地传给B，C两人中的某一人，以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人．

(1)、求两次传球后，球恰在B手中的概率；

(2)、求三次传球后，球恰在A手中的概率．

查看试题解析
25. 如图，已知直线y=x+k和双曲线y= $\frac{k + 1}{x}$ （k为正整数）交于A，B两点．

(1)、当k=1时，求A、B两点的坐标；

(2)、当k=2时，求△AOB的面积；

(3)、当k=1时，△OAB的面积记为S₁ ，当k=2时，△OAB的面积记为S₂ ， …，依此类推，当k=n时，△OAB的面积记为S_n ，若S₁+S₂+…+S_n= $\frac{133}{2}$ ，求n的值．

查看试题解析
26. 阅读材料：
在一个三角形中，各边和它所对角的正弦的比相等， $\frac{a}{s i n A}$ = $\frac{b}{s i n B}$ = $\frac{c}{s i n C}$ ，利用上述结论可以求解如下题目：
在△ABC中，∠A、∠B、∠C的对边分别为a，b，c．若∠A=45°，∠B=30°，a=6，求b．
解：在△ABC中，∵ $\frac{a}{s i n A}$ = $\frac{b}{s i n B}$ ∴b= $\frac{a s i n B}{s i n A}$ = $\frac{6 s i n 30 °}{s i n 45 °}$ = $\frac{6 \times \frac{1}{2}}{\frac{\sqrt{2}}{2}}$ =3 $\sqrt{2}$ ．
理解应用：
如图，甲船以每小时30 $\sqrt{2}$ 海里的速度向正北方向航行，当甲船位于A₁处时，乙船位于甲船的北偏西105°方向的B₁处，且乙船从B₁处按北偏东15°方向匀速直线航行，当甲船航行20分钟到达A₂时，乙船航行到甲船的北偏西120°方向的B₂处，此时两船相距10 $\sqrt{2}$ 海里．

(1)、判断△A₁A₂B₂的形状，并给出证明；

(2)、求乙船每小时航行多少海里？

查看试题解析
27. 如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O．点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交AB右侧的圆弧于点E．在射线CD上取点F，使DF= $\frac{3}{2}$ CD，以DE，DF为邻边作矩形DEGF．设AQ=3x．

(1)、用关于x的代数式表示BQ，DF．

(2)、当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长．

(3)、在点P的整个运动过程中，
①当AP为何值时，矩形DEGF是正方形？
②作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长（直接写出答案）．

查看试题解析
28. 如图，抛物线y=x²﹣4x与x轴交于O，A两点，P为抛物线上一点，过点P的直线y=x+m与对称轴交于点Q．

(1)、这条抛物线的对称轴是，直线PQ与x轴所夹锐角的度数是；

(2)、若两个三角形面积满足S_△_POQ= $\frac{1}{3}$ S_△_PAQ ，求m的值；

(3)、当点P在x轴下方的抛物线上时，过点C（2，2）的直线AC与直线PQ交于点D，求：①PD+DQ的最大值；②PD•DQ的最大值．

查看试题解析

金额（元）	20	30	35	50	100
学生数（人）	3	7	5	15	10