2015-2016学年广西防城港市防城区七年级下学期期中数学试卷

试卷更新日期：2016-08-04 类型：期中考试

进入出卷网下载

一、单选题

1. 9的平方根是（　　）

A、±3 B、± $\frac{1}{3}$ C、3 D、-3

查看试题解析
2.
如图，能判定EC∥AB的条件是（　　）

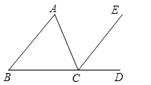A、∠B=∠ACE B、∠A=∠ECD C、∠B=∠ACB D、∠A=∠ACE

查看试题解析
3.
如图，点A（﹣2，1）到y轴的距离为（　　）

A、-2 B、1 C、2 D、 $\sqrt{5}$

查看试题解析
4.
如图，图中∠α的度数等于（　　）

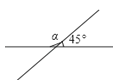A、135° B、125° C、115° D、105°

查看试题解析
5. 如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（）

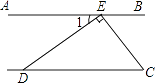A、34° B、56° C、66° D、54°

查看试题解析
6.
如图，在直角坐标系中，卡片盖住的数可能是（　　）

A、（2，3） B、（﹣2，1） C、（﹣2，﹣2.5） D、（3，﹣2）

查看试题解析
7. 若|3﹣a|+ $\sqrt{2 + b}$ =0，则a+b的值是（　　）

A、2 B、1 C、0 D、-1

查看试题解析
8. 估算 $\sqrt{27}$ ﹣2的值（　　）

A、在1到2之间 B、在2到3之间 C、在3到4之间 D、在4到5之间

查看试题解析
9. 已知点P位于y轴右侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P坐标是（　　）

A、（﹣3，4） B、（3，4） C、（﹣4，3） D、（4，3）

查看试题解析
10. 在平面直角坐标系中，将点B（﹣3，2）向右平移5个单位长度，再向下平移3个单位长度后与点A（x，y）重合，则点A的坐标是（　　）

A、（2，5） B、（﹣8，5） C、（﹣8，﹣1） D、（2，﹣1）

查看试题解析
11.
如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（　　）

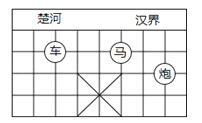A、（3，2） B、（﹣3，2） C、（3，﹣2） D、（﹣3，﹣2）

查看试题解析
12.
如图，直线AC∥BD，AO、BO分别是∠BAC、∠ABD的平分线，那么∠BAO与∠ABO之间的大小关系一定为（　　）

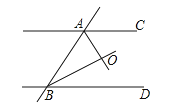A、互余 B、相等 C、互补 D、不等

查看试题解析

二、填空题

13.
如图，直线a∥b，∠1=125°，则∠2的度数为

查看试题解析
14. 4的算术平方根是，9的平方根是，﹣27的立方根是

查看试题解析
15. 将实数 $\sqrt{5}$ ， π，0，﹣6由小到大用“＜”号连起来，可表示为

查看试题解析
16.
如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为．

查看试题解析
17.
如图，在长20米，宽10米的长方形草地内修建了宽2米的道路，则草地的面积为米²

查看试题解析
18. 观察下列各式： $\sqrt{1 + \frac{1}{3}}$ =2 $\sqrt{\frac{1}{3}}$ ， $\sqrt{2 + \frac{1}{4}}$ =3 $\sqrt{\frac{1}{4}}$ ， $\sqrt{3 + \frac{1}{5}}$ =4 $\sqrt{\frac{1}{5}}$ ， …请你找出其中规律，并将第n（n≥1）个等式写出来

查看试题解析
19. 把下列各数的序号填在相应的横线上．①﹣0.3，②0，③ $\sqrt{5}$ ， ④π² ， ⑤|﹣2|，⑥ $\sqrt[3]{- 8}$ ， ⑦3.1010010001…（每两个1之间多一个0），⑧﹣ $\frac{22}{7}$
分数：，整数：，无理数：

查看试题解析
20.
如图，AB和CD相交于点O，∠C=∠1，∠D=∠2，求证：∠A=∠B．
证明：∵∠C=∠1，∠D=∠2（已知）
又∵∠1=∠2（）
∴ （）
∴AC∥BD（）
∴ （两直线平行，内错角相等）

查看试题解析

三、综合题

21.
我们在学习“实数”时，画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交x轴于点A”，请根据图形回答下列问题：

(1)、线段OA的长度是多少？（要求写出求解过程）

(2)、这个图形的目的是为了说明什么？

(3)、这种研究和解决问题的方式，体现了的数学思想方法．
（将下列符合的选项序号填在横线上）
A、数形结合；B、代入；C、换元；D、归纳．

查看试题解析

四、解答题

22.
如图，已知：AB∥DE，∠1=∠2，直线AE与DC平行吗？请说明理由．

查看试题解析
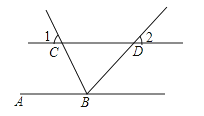
23.
如图，直线AB∥CD，BC平分∠ABD，∠1=65°，求∠2的度数．

查看试题解析
24.
如图，△A₁B₁C₁是△ABC向右平移4个单位长度后得到的，且三个顶点的坐标分别为A₁（1，1），B₁（4，2），C₁（3，4）．
（1）请画出△ABC，并写出点A，B，C的坐标；
（2）求出△AOA₁的面积．

查看试题解析
25.
位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示．
（1）建立适当的平面直角坐标系，使医院的坐标为（3，0）并写出小明家、学校、游乐场的坐标；
（2）根据蜀河大坝蓄水工程需要，小明家及学校、医院、游乐场需要等距离整体迁移，已知迁移后新的小明家、学校、游乐场、医院分别用A、B、C、D表示，且这四点的坐标分别用原来各地点的横坐标都减去5、纵坐标都加上2 得到，请先在图中描出A、B、C、D的位置，画出四边形ABCD，
然后说明四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过怎样平移得到的？

查看试题解析
26.
如图，已知平面内有两条直线AB、CD，且AB∥CD，P为一动点．
（1）当点P移动到AB、CD之间时，如图（1），这时∠P与∠A、∠C有怎样的关系？证明你的结论．
（2）当点P移动到如图（2）的位置时，∠P与∠A、∠C又有怎样的关系？请证明你的结论．

查看试题解析