2015-2016学年黑龙江省哈尔滨市道里区九年级上学期期末数学试卷
试卷更新日期:2016-08-04 类型:期末考试
一、单选题
-
1. 点A(﹣3,5)关于原点的对称点的坐标为( )A、(3,5) B、(﹣3,﹣5) C、(3,﹣5) D、(5,﹣3)2. “珍惜生命,注意安全”是一永恒的话题.在现代化的城市,交通安全晚不能被忽视,下列几个图形是国际通用的几种交通标志,其中不是中心对称图形是( )A、禁止行车
 B、禁止行人通行
B、禁止行人通行 C、禁止车辆长时间停放
C、禁止车辆长时间停放 D、禁止车辆临时或长时间停放
D、禁止车辆临时或长时间停放 3. 在Rt△ABC中,∠C=90°,若sinA= , 则cosB的值是( )A、 B、 C、 D、4. 抛物线y=﹣5(x﹣2)2+3的顶点坐标是( )A、(2,3) B、(﹣2,3) C、(2,﹣3) D、(﹣2,﹣3)5. 在反比例函数 y=的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )A、k>1 B、k>0 C、k≥1 D、k<16.
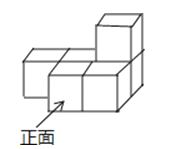
3. 在Rt△ABC中,∠C=90°,若sinA= , 则cosB的值是( )A、 B、 C、 D、4. 抛物线y=﹣5(x﹣2)2+3的顶点坐标是( )A、(2,3) B、(﹣2,3) C、(2,﹣3) D、(﹣2,﹣3)5. 在反比例函数 y=的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )A、k>1 B、k>0 C、k≥1 D、k<16.如图所示的几何体是由六个相同的小正方体组合而成的,它的俯视图是( )
 A、
A、 B、
B、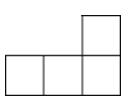 C、
C、 D、
D、 7. 如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )
7. 如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,下列各式中错误的是( )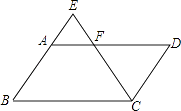 A、 B、 C、 D、8.
A、 B、 C、 D、8.如图,AB为⊙O的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
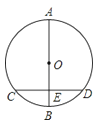 A、6 B、8 C、2 D、49. 在函数y=(k<0)的图象上有三点Al(xl , y1)、A2(x2 , y2)、A3(x3 , y3),已知xl<x2<0<x3 , 则下列各式正确的是( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y3<y1<y210.
A、6 B、8 C、2 D、49. 在函数y=(k<0)的图象上有三点Al(xl , y1)、A2(x2 , y2)、A3(x3 , y3),已知xl<x2<0<x3 , 则下列各式正确的是( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y3<y1<y210.已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=﹣1,给出下列结论:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.其中正确的结论有( )
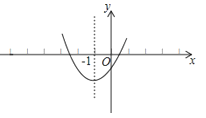 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 在Rt△ABC中,∠C=90°,AC=1,AB=2,则sinA=12. 将二次函数y=x2+4x﹣2配方成y=(x﹣h)2+k的形式,则y= .13. 已知点M(﹣2,3)在双曲线y=上,k的值为14. 一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形的半径为 cm.15. 将抛物线y=2x2向右平移3个单位,再向下平移4个单位后所得到的抛物线解析式为16. 在一个不透明的口袋中装有除颜色外其它都相同的5个红球和3个自球,任意从口袋中摸出一个球来,摸到白球的概率为17.
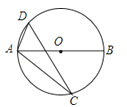
如图,AB为⊙0的直径,点C、D在⊙0上,且∠ADC=52°,则∠BAC=°.
 18.
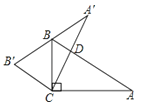
18.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角∠A CA′的度数为 .
 19. 圆的内接等腰三角形ABC,圆的半径为10,如果底边BC的长为16,那么△ABC的面积为20.
19. 圆的内接等腰三角形ABC,圆的半径为10,如果底边BC的长为16,那么△ABC的面积为20.在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F= , FC=FN,EN= , 则EF=

三、计算题
-
21. 先化简,再求代数式的值,其中a=3tan30°+1,b=cos45°.
四、解答题
-
22.
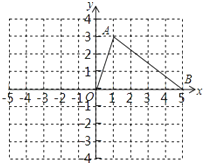
如图,网格中每个小正方形的顶点叫格点,△OAB的顶点的坐标分别为O(0,0)、A(1,3)、B(5,0).
(1)请画出与△OAB关于原点对称的△OCD;(其中A的对称点为C,B的对称点为D)
(2)在(1)的条件下,连接BC、DA,请画出一条直线MN(不与直线AC和坐标轴重合),将四边形ABCD的面积分成相等的两部分,其中M、N分别在AD和BC上,且M、N均为格点,并直接写出直线MN的解析式(写出一个即可).
 23.
23.如图,小平为了测量学校教学楼的高度,她先在A处利用测角仪测得楼顶C的仰角为30°,再向楼的方向直行50米到达B处,又测得楼顶C的仰角为60度.已知测角仪的高度是1.2米,请你帮助小平计算出学校教学楼的高度CO.()
 24.
24.已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH
 25. 小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
25. 小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用)
26.已知:AB是⊙O的直径,DA、DC分别是⊙O的切线,点A、C是切点,连接DO交弧AC于点E,连接AE、CE.
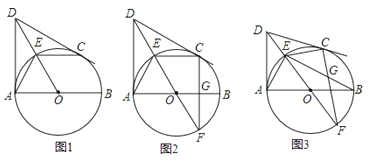
(1)如图1,求证:EA=EC;
(2)如图2,延长DO交⊙O于点F,连接CF、BE交于点G,求证:∠CGE=2∠F;
(3)如图3,在(2)的条件下,DE=AD,EF=2 , 求线段CG的长.
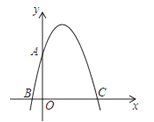
27.如图,在平面直角坐标系中,点0为坐标原点,抛物线y=ax2+bx+4与y轴交于点A,与x轴交于点B、C(点B在点C左侧),且OA=OC=4OB.
(1)求a,b的值;
(2)连接AB、AC,点P是抛物线上第一象限内一动点,且点P位于对称轴右侧,
过点P作PD⊥AC于点E,分别交x、y轴于点D、H,过点P作PG∥AB交AC于点F,交x轴于点G,设P(x,y),线段DG的长为d,求d与x之间的函数关系(不要求写出自变量x的取值范围);
(3)在(2)的条件下,当时,连接AP并延长至点M,连接HM交AC于点S,点R是抛物线上一动点,当△ARS为等腰直角三角形时.求点R的坐标和线段AM的长.
-