2015-2016学年北京市燕山区九年级上学期期末数学试卷
试卷更新日期:2016-08-04 类型:期末考试
一、单选题
-
1. 二次函数y=(x﹣1)2+2的最小值是( )A、-2 B、-1 C、1 D、22. 下面四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下面的几何体中,主视图为三角形的是( )A、
3. 下面的几何体中,主视图为三角形的是( )A、 B、
B、 C、
C、 D、
D、 4. 若△ABC∽△DEF,相似比为1:3,则△ABC与△DEF的面积比为( )A、1:9 B、1:3 C、1:2 D、1:5.
4. 若△ABC∽△DEF,相似比为1:3,则△ABC与△DEF的面积比为( )A、1:9 B、1:3 C、1:2 D、1:5.有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为( )
 A、 B、 C、 D、6.
A、 B、 C、 D、6.如图,AB是⊙O的直径,C,D是圆上两点,∠AOC=50°,则∠D等于( )
 A、25° B、30° C、40° D、50°7.
A、25° B、30° C、40° D、50°7.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
 A、 B、 C、 D、8.
A、 B、 C、 D、8.已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
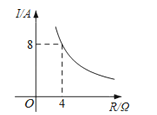 A、I= B、I= C、I= D、I=-9.
A、I= B、I= C、I= D、I=-9.某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:≈1.4)( )
 A、
A、 B、
B、 C、
C、 D、
D、 10.
10.一个寻宝游戏的寻宝通道如图1所示,四边形ABCD为矩形,且AB>AD>AB,为记录寻宝者的行进路线,在AB的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )
 A、O→D→C→B B、A→B→C C、D→O→C→B D、B→C→O→A
A、O→D→C→B B、A→B→C C、D→O→C→B D、B→C→O→A二、填空题
-
11. 点P(﹣3,4)关于原点对称的点的坐标是12. 关于x的一元二次方程ax2+bx﹣2015=0有一个根为x=1,写出一组满足条件的实数a,b的值:a= ,b=13. 某农科院在相同条件下做了某种玉米种子发芽率的试验,结果如下:
种子总数
100
400
800
1000
3500
7000
9000
14000
发芽种子数
91
354
716
901
3164
5613
8094
12614
发芽的频率
0.91
0.885
0.895
0.901
0.904
0.902
0.899
0.901
则该玉米种子发芽的概率估计值为 (结果精确到0.1).
14.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门 步而见木.
 15. 老师在课堂上出了一个问题:若点A(﹣2,y1),B(1,y2)和C(4,y3)都在反比例函数y=的图象上,比较y1 , y2 , y3的大小.
15. 老师在课堂上出了一个问题:若点A(﹣2,y1),B(1,y2)和C(4,y3)都在反比例函数y=的图象上,比较y1 , y2 , y3的大小.小明是这样思考的:当k<0时,反比例函数的图象是y随x的增大而增大的,并且﹣2<1<4,所以y1<y2<y3 .
你认为小明的思考 (填“正确”和“不正确”),理由是 .
16.阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.
小芸的作法如下:
①取AB=c,作AB的垂直平分线交AB于点O;
②以点O为圆心,OB长为半径画圆;
③以点B为圆心,a长为半径画弧,与⊙O交于点C;
④连接BC,AC.
则Rt△ABC即为所求.
老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是

三、计算题
-
17. 计算:cos45°﹣tan30°•sin60°.18. 解方程:x2﹣3x﹣1=0.
四、解答题
-
19.
如图,⊙O的半径为5,AB为弦,OC⊥AB,交AB于点D,交⊙O于点C,CD=2,求弦AB的长.
 20.
20.如图,△ABC中,CD是边AB上的高,且= .
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
 21.
21.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1 .
(1)在网格中画出△AB1C1;
(2)计算点B旋转到B1的过程中所经过的路径长.(结果保留π)
 22. 已知二次函数y=2x2﹣8x.
22. 已知二次函数y=2x2﹣8x.(1)用配方法将y=2x2﹣8x化成y=a(x﹣h)2+k的形式;
(2)求出该二次函数的图象与x轴的交点A,B的坐标(A在B的左侧);
(3)将该二次函数的图象沿x轴向左平移2个单位,再沿y轴向上平移3个单位,请直接写出得到的新图象的函数表达式.
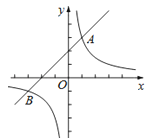
23.如图,一次函数y=x+2的图象与反比例函数y=(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
(1)求反比例函数y=(k≠0)的表达式;
(2)若P是y轴上一点,且满足△ABP的面积为6,求点P的坐标.
 24.
24.北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:≈1.41,≈1.73,≈2.45)
 25.
25.如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D= , 求AE的长.
 26.
26.有这样一个问题:探究函数y=+x的图象与性质.
小东根据学习函数的经验,对函数y=+x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=+x的自变量x的取值范围是;
(2)下表是y与x的几组对应值.

求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可)
 27.
27.在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(﹣1,t),B(3,t),与y轴交于点C(0,﹣1).一次函数y=x+n的图象经过抛物线的顶点D.
(1)求抛物线的表达式;
(2)求一次函数y=x+n的表达式;
(3)将直线l:y=mx+n绕其与y轴的交点E旋转,使当﹣1≤x≤1时,直线l总位于抛物线的下方,请结合函数图象,求m的取值范围.
 28.
28.如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.

(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为 , 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
29.在平面直角坐标系xOy中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点P′为射线CP上一点,满足CP•CP′=r2 , 则称点P′为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点P′的示意图.

(1)如图2,当⊙O的半径为1时,分别求出点M(1,0),N(0,2),T( , )关于⊙O的反演点M′,N′,T′的坐标;
(2)如图3,已知点A(1,4),B(3,0),以AB为直径的⊙G与y轴交于点C,D(点C位于点D下方),E为CD的中点.
①若点O,E关于⊙G的反演点分别为O′,E′,求∠E′O′G的大小;
②若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为Q′,请直接写出线段GQ′的长度.