2015-2016学年北京市海淀区九年级上学期期末数学试卷
试卷更新日期:2016-08-04 类型:期末考试
一、单选题
-
1. 在△ABC中,∠C=90°,BC=3,AB=5,则sinA的值是( )A、 B、 C、 D、2.
如图,⊙O是△ABC的外接圆,若∠AOB=100°,则∠ACB的度数是( )
 A、40° B、50° C、60° D、80°3. 抛物线y=(x﹣2)2+1的顶点坐标是( )A、(﹣2,﹣1) B、(﹣2,1) C、(2,﹣1) D、(2,1)4. 若点A(a,b)在双曲线y=上,则代数式ab﹣4的值为( )A、-12 B、-7 C、-1 D、15. 如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCF的面积比为( )
A、40° B、50° C、60° D、80°3. 抛物线y=(x﹣2)2+1的顶点坐标是( )A、(﹣2,﹣1) B、(﹣2,1) C、(2,﹣1) D、(2,1)4. 若点A(a,b)在双曲线y=上,则代数式ab﹣4的值为( )A、-12 B、-7 C、-1 D、15. 如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCF的面积比为( )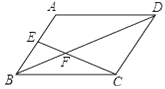 A、 B、 C、 D、6. 抛物线y=2x2向左平移1个单位,再向下平移3个单位,则平移后的抛物线的解析式为( )A、y=2(x+1)2+3 B、y=2(x+1)2﹣3 C、y=2(x﹣1)2﹣3 D、y=2(x﹣1)2+37. 已知点(x1 , y1)、(x2 , y2)、(x3 , y3)在双曲线y=上,当x1<0<x2<x3时,y1、y2、y3的大小关系是( )A、y1<y2<y3 B、y1<y3<y2 C、y3<y1<y2 D、y2<y3<y18.
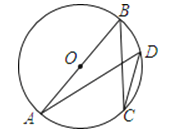
A、 B、 C、 D、6. 抛物线y=2x2向左平移1个单位,再向下平移3个单位,则平移后的抛物线的解析式为( )A、y=2(x+1)2+3 B、y=2(x+1)2﹣3 C、y=2(x﹣1)2﹣3 D、y=2(x﹣1)2+37. 已知点(x1 , y1)、(x2 , y2)、(x3 , y3)在双曲线y=上,当x1<0<x2<x3时,y1、y2、y3的大小关系是( )A、y1<y2<y3 B、y1<y3<y2 C、y3<y1<y2 D、y2<y3<y18.如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,cosD= , 则AB的长为( )
 A、 B、 C、 D、129. 在平面直角坐标系xOy中,A为双曲线y=-上一点,点B的坐标为(4,0).若△AOB的面积为6,则点A的坐标为( )A、(﹣4,) B、(4,-) C、(﹣2,3)或(2,﹣3) D、(﹣3,2)或(3,﹣2)10.
A、 B、 C、 D、129. 在平面直角坐标系xOy中,A为双曲线y=-上一点,点B的坐标为(4,0).若△AOB的面积为6,则点A的坐标为( )A、(﹣4,) B、(4,-) C、(﹣2,3)或(2,﹣3) D、(﹣3,2)或(3,﹣2)10.如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )
 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
11. 请写一个图象在第二、四象限的反比例函数解析式:12. 已知关于x的方程x2﹣6x+m=0有两个不相等的实数根,则m的取值范围是13.
如图,在平面直角坐标系xOy中,△ABC与△A′B′C′顶点的横、纵坐标都是整数.若△ABC与△A′B′C′是位似图形,则位似中心的坐标是 .
 14.
14.如图,正比例函数y=mx(m≠0)与反比例函数y=的图象交于A、B两点,若点A的坐标为(1,2),则点B的坐标是
 15. 古算趣题:“笨人执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭.有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足.借问竿长多少数,谁人算出我佩服.”若设竿长为x尺,则可列方程为 .16.
15. 古算趣题:“笨人执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭.有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足.借问竿长多少数,谁人算出我佩服.”若设竿长为x尺,则可列方程为 .16.正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
(1)如图,若tanB=2,则的值为
(2)将△ABC绕点D旋转得到△A′B′C′,连接BB′、CC′.若 , 则tanB的值为

三、解答题
-
17. 计算:sin30°+3tan60°﹣cos245°18. 解方程:x2+2x﹣5=019.
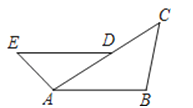
如图,D是AC上一点,DE∥AB,∠B=∠DAE.求证:△ABC∽△DAE.
 20. 已知m是方程x2+x﹣1=0的一个根,求代数式(m+1)2+(m+1)(m﹣1)的值.21. 已知二次函数y=x2+bx+8的图象与x轴交于A、B两点,点A的坐标为(﹣2,0),求点B的坐标.22.
20. 已知m是方程x2+x﹣1=0的一个根,求代数式(m+1)2+(m+1)(m﹣1)的值.21. 已知二次函数y=x2+bx+8的图象与x轴交于A、B两点,点A的坐标为(﹣2,0),求点B的坐标.22.如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米.
(1)求y与x之间的函数关系式?(不要求写自变量的取值范围);
(2)求矩形ABCD的最大面积.
 23.
23.如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
 24.
24.如图,在平面直角坐标系xOy中,双曲线y=与直线y=kx﹣2交于点A(3,1).
(1)求直线和双曲线的解析式;
(2)直线y=kx﹣2与x轴交于点B,点P是双曲线y=上一点,过点P作直线PC∥x轴,交y轴于点C,交直线y=kx﹣2于点D.若DC=2OB,写出点P的坐标.
 25. 如图,小嘉利用测角仪测量塔高,他分别站在 、 两点测得塔顶的仰角 为10米.已知小嘉的眼睛距地面的高度 为1.5米,计算塔的高度.(参考数据: 取0.8, 取0.6, 取1.2)
25. 如图,小嘉利用测角仪测量塔高,他分别站在 、 两点测得塔顶的仰角 为10米.已知小嘉的眼睛距地面的高度 为1.5米,计算塔的高度.(参考数据: 取0.8, 取0.6, 取1.2)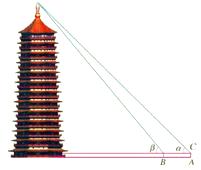 26.
26.如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.
(1)求证:∠CBE=∠A;
(2)若⊙O的直径为5,BF=2,tanA=2,求CF的长.
 27.
27.如图,在平面直角坐标系xOy中,定义直线x=m与双曲线yn=的交点Am , n(m、n为正整数)为“双曲格点”,双曲线yn=在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
 (1)、①“双曲格点”A2 , 1的坐标为 ;②若线段A4 , 3A4 , n的长为1个单位长度,则n= ;(2)、图中的曲线f是双曲线y1=的一条“派生曲线”,且经过点A2 , 3 , 则f的解析式为y=(3)、画出双曲线y3=的“派生曲线”g(g与双曲线y3=不重合),使其经过“双曲格点”A2 , a、A3 , 3、A4 , b .28.
(1)、①“双曲格点”A2 , 1的坐标为 ;②若线段A4 , 3A4 , n的长为1个单位长度,则n= ;(2)、图中的曲线f是双曲线y1=的一条“派生曲线”,且经过点A2 , 3 , 则f的解析式为y=(3)、画出双曲线y3=的“派生曲线”g(g与双曲线y3=不重合),使其经过“双曲格点”A2 , a、A3 , 3、A4 , b .28.(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,求△BCD的周长为;
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②在图3中补全图形,求∠EOF的度数;
③若 , 求的值

四、综合题
-
29.
在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).
 (1)、当点A的坐标为(0,0),点B的坐标为(1,3)时,特征点C的坐标为 .
(1)、当点A的坐标为(0,0),点B的坐标为(1,3)时,特征点C的坐标为 .
(2)、若抛物线y=ax2+bx如图所示,请在所给图中标出点A、点B的位置;(3)、设抛物线y=ax2+bx的对称轴与x轴交于点D,其特征直线交y轴于点E,点F的坐标为(1,0),DE∥CF.①若特征点C为直线y=﹣4x上一点,求点D及点C的坐标 ;
②若<tan∠ODE<2,则b的取值范围是 .