2015-2016学年广东省韶关市南雄市七年级上学期末数学试卷
试卷更新日期:2016-08-03 类型:期末考试
一、单选题
-
1. 2015的相反数是( )A、 B、-2015 C、2015 D、-2. 在﹣4,0,2.5,|﹣3|这四个数中,最大的数是( )A、-4 B、0 C、2.5 D、|﹣3|3. 我国作家莫言获得诺贝尔文学奖之后,他的代表作品《蛙》的销售量就比获奖之前增长了180倍,达到2100000册.把2100000用科学记数法表示为( )A、0.21×108 B、21×106 C、2.1×107 D、2.1×1064. 下列方程为一元一次方程的是( )A、y+3=0 B、x+2y=3 C、x2=2x D、+y=25. 已知∠A=65°,则∠A的补角等于( )A、125° B、105° C、115° D、95°6. 下列各式正确的是( )A、﹣8+5=3 B、(﹣2)3=6 C、﹣(a﹣b)=﹣a+b D、2(a+b)=2a+b7.
如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
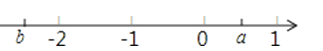 A、b﹣a>0 B、a+b<0 C、ab<0 D、b<a8.
A、b﹣a>0 B、a+b<0 C、ab<0 D、b<a8.将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )
 A、
A、 B、
B、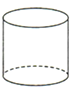 C、
C、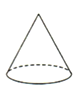 D、
D、 9. 一个长方形的周长是30厘米,若长方形的一边用字母x(厘米)表示,则该长方形的面积是( )A、x(30﹣2x)平方厘米 B、x(30﹣x)平方厘米 C、x(15﹣x)平方厘米 D、x(15+x)平方厘米10. 某商人在一次买卖中均以120元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )A、赚16元 B、赔16元 C、不赚不赔 D、无法确定
9. 一个长方形的周长是30厘米,若长方形的一边用字母x(厘米)表示,则该长方形的面积是( )A、x(30﹣2x)平方厘米 B、x(30﹣x)平方厘米 C、x(15﹣x)平方厘米 D、x(15+x)平方厘米10. 某商人在一次买卖中均以120元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )A、赚16元 B、赔16元 C、不赚不赔 D、无法确定二、填空题
-
11. 如果“节约10%”记作+10%,那么“浪费6%”记作:12. 按四舍五入法则取近似值:
2.086≈ (精确到百分位).
0.03445≈ (精确到0.001)
13. 若﹣5xny2与12x3y2m是同类项,则m= ,n=14. 已知5是关于x的方程3x﹣2a=7的解,则a的值为15.如图,AB,CD相交于点O,OE⊥AB,垂足为O,∠COE=44°,则∠AOD=
 16. 已知线段AB=acm,A1平分AB,A2平分AA1 , A3平分AA2 , …,An平分AAn﹣1 , 则AAn=cm.
16. 已知线段AB=acm,A1平分AB,A2平分AA1 , A3平分AA2 , …,An平分AAn﹣1 , 则AAn=cm.三、计算题
-
17. 计算:﹣12014﹣6÷(﹣2)×|﹣|.18.
如图,已知平面上有四个点A,B,C,D.
(1)连接AB,并画出AB的中点P;
(2)作射线AD;
(3)作直线BC与射线AD交于点E.
 19. 解方程: .20. 已知(x+2)2+|y﹣|=0,求5x2y﹣[2x2y﹣(xy2﹣2x2y)﹣4]﹣2xy2的值.
19. 解方程: .20. 已知(x+2)2+|y﹣|=0,求5x2y﹣[2x2y﹣(xy2﹣2x2y)﹣4]﹣2xy2的值.四、解答题
-
21. 列方程解应用题:七、八年级学生分别到雷锋、毛泽东纪念馆参观,共590人,到毛泽东纪念馆的人数是到雷锋纪念馆人数的2倍多56人,到雷锋纪念馆参观的人数有多少人?22. 某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期
一
二
三
四
五
六
日
增减/辆
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总生产量是多少?比原计划增加了还是减少了?增减数为多少?
23. 某市出租车的收费标准是:行程不超过3千米起步价为10元,超过3千米后每千米增收1.8元.某乘客出租车x千米.(1)试用关于x的代数式分情况表示该乘客的付费.
(2)如果该乘客坐了8千米,应付费多少元?
(3)如果该乘客付费26.2元,他坐了多少千米?
24.如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
 (1)、如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?(2)、如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果)(3)、如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON= (直接写出结果).25.
(1)、如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?(2)、如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果)(3)、如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON= (直接写出结果).25.如图,已知数轴上点A,B是数轴上的一点,AB=12,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数,经t秒后点P走过的路程为(用含t的代数式表示);
(2)若在动点P运动的同时另一动点Q从点B也出发,并以每秒4个单位长度的速度沿数轴向左匀速运动,问经多少时间点P就能追上点Q?
(3)若M为AP的中点,N为BP的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.