2015-2016学年北京市延庆县七年级上学期末数学试卷
试卷更新日期:2016-08-03 类型:期末考试
一、单选题
-
1. ﹣的相反数是( )A、 B、- C、2 D、-22. 第30届延庆冰雪欢乐节于2015年12月20日开幕.本届冰雪欢乐节以“冰雪延庆,激情冬奥”为主题,将持续至2016年2月底.在70余天的时间里,延庆将举办冰雪赛事、冰雪培训、冰雪旅游、文化宣传4大类20项活动,据不完全统计,截止2016年1月4日,冰雪节期间,延庆乡村旅游收入超过2350000元.将2350000用科学记数法表示应为( )A、2.35×107 B、2.35×106 C、23.5×106 D、23.5×1053. 下面的说法正确的是( )A、﹣a表示负数 B、﹣2是单项式 C、的系数是3 D、x++1是多项式4. 下列计算正确的是( )A、7a+a=7a2 B、5y﹣3y=2 C、3x2y﹣2yx2=x2y D、3a+2b=5ab5. 下列生活、生产现象中,其中可用“两点之间,线段最短”来解释的现象有( )
①用两颗钉子就可以把木条固定在墙上;
②植树时,只要栽下两棵树,就可以把同一行树栽在同一直线上;
③从A到B架设电线,总是尽可能沿线段AB架设;
④把弯曲的公路改直,就能缩短路程.
A、①② B、①③ C、②④ D、③④6. 若代数式﹣2ax+7b4与代数式3a4b2y是同类项,则xy的值是( )A、9 B、-9 C、4 D、-47. 某商人在一次买卖中均以120元卖出两件商品,其中一件赚了20%,一件赔了20%,在这次交易中,该商人( )A、不赔不赚 B、赚了10元 C、赔了10元 D、赔了30元8.已知数a,b在数轴上表示的点的位置如图所示,则下列结论正确的是( )
 A、a+b>0 B、a﹣b>0 C、a•b>0 D、a•b<09. 将一副直角三角尺按如图所示的不同方式摆放,则图中∠α与∠β相等的是( )
A、a+b>0 B、a﹣b>0 C、a•b>0 D、a•b<09. 将一副直角三角尺按如图所示的不同方式摆放,则图中∠α与∠β相等的是( )
A、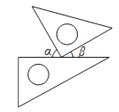 B、
B、 C、
C、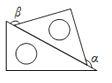 D、
D、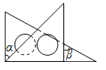 10.
10.按下面的程序计算,

当输入x=100时,输出结果为501;当输入x=20时,输出结果为506;如果开始输入的值x为正数,最后输出的结果为656,那么满足条件的x的值最多有( )
A、5个 B、4个 C、3个 D、2个二、填空题
-
11. 如果∠A=34°15′,那么∠A的余角等于12.
如图是某几何体的展开图,那么这个几何体是
 13. 写出一个只含有字母x,y的二次三项式14. 小明在解一元一次方程■x﹣3=2x+9时,不小心把墨汁滴在作业本上,其中未知数x前的系数看不清了,他便问邻桌,但是邻桌只告诉他,方程的解是x=﹣2(邻桌的答案是正确的),小明由此知道了被墨水遮住的x的系数,请你帮小明算一算,被墨水遮住的系数是15. 刘谦的魔术表演风靡全世界,很多同学非常感兴趣,也学起了魔术.小华把任意有理数对(x,y)放进装有计算装置的魔术盒,会得到一个新的有理数x+y2+1.
13. 写出一个只含有字母x,y的二次三项式14. 小明在解一元一次方程■x﹣3=2x+9时,不小心把墨汁滴在作业本上,其中未知数x前的系数看不清了,他便问邻桌,但是邻桌只告诉他,方程的解是x=﹣2(邻桌的答案是正确的),小明由此知道了被墨水遮住的x的系数,请你帮小明算一算,被墨水遮住的系数是15. 刘谦的魔术表演风靡全世界,很多同学非常感兴趣,也学起了魔术.小华把任意有理数对(x,y)放进装有计算装置的魔术盒,会得到一个新的有理数x+y2+1.例如:把(﹣1,2)放入其中,就会得到﹣1+22+1=4.现将有理数对(3,﹣2)放入其中,得到的有理数是 .若将正整数对放入其中,得到的值是6,则满足条件的所有的正整数对(x,y)为
16.毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究:

(1)六边形第5层的几何点数是 ;第n层的几何点数是 .
(2)在第 层时,六边形的几何点数是三角形的几何点数的3.5倍.
三、计算题
-
17. 计算:
(1)8﹣(﹣2)﹣(+3)+(﹣1)
(2)(﹣12)÷(+4)﹣(﹣2)×(﹣3)
(3)
(4) .
18. 先化简,再求值:2x﹣3y﹣3(x﹣2y),其中x=﹣2,y=1.19. 解方程:(1)3x+7=23﹣x
(2)3(x﹣2)=x﹣(2x﹣1)
(3) .
20. 解不等式组: .四、解答题
-
21. 自2010年延庆区举办骑游大会以来,到延庆骑游的人越来越多,延庆区人民政府决定投放公租自行车供市民使用.到2015年底,投放在东湖、西湖自行车租赁点的公租自行车共有550辆,西湖自行车租赁点的公租自行车数量是东湖自行车租赁点的公租自行车数量的2倍少20辆.这两个公租自行车租赁点各有多少辆自行车?22.
如图:A,B,C,D是平面上四个点,按下列要求画出图形.
(1)连接BD;
(2)作射线CB,与DA的延长线交于点E;
(3)过C作BD的垂线,垂足为F.
 23. 如图,已知点C是线段AB的中点,AB=9,若E是直线AB上一点,且BE=2,
23. 如图,已知点C是线段AB的中点,AB=9,若E是直线AB上一点,且BE=2,(1)请依题意补全图形;
(2)求CE的长.
 24.
24.延庆区某中学七年级(1)(2)两个班共104人,要去延庆地质博物馆进行社会大课堂活动,老师指派小明到网上查阅票价信息,小明查得票价如图:

其中(1)班不足50人,经估算,如果两个班都以班为单位购票,一共应付1240元.
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可以省多少钱?
(3)如果七年级(1)班单独组织去博物馆参观,你认为如何购票最省钱?
25. 已知∠AOB=60°,从点O引射线OC,使∠AOC=40°,作∠AOC的角平分线OD,(1)依题意画出图形;
(2)求∠BOD的度数.
26. 已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.(1)如果点P到点M、点N的距离相等,那么x的值是多少?
(2)数轴上是否存在点P,使点P到点M、点N的距离之和是7?如果存在,求出x的值;如果不存在,请说明理由;
(3)如果点P以每秒钟6个单位长度的速度从点O向右运动时,点M和点N分别以每秒钟1个单位长度和每秒钟3个单位长度的速度也向右运动,且三点同时出发,那么经过几秒钟,点P到点M、点N的距离相等.