2015-2016学年湖北省武汉市青山区八年级上学期末数学试卷

试卷更新日期：2016-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图案中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 要使分式 $\frac{1}{x + 2}$ 有意义，则x的取值应满足（　　）

A、x=﹣2 B、x≠2 C、x＞﹣2 D、x≠﹣2

查看试题解析
3. 下列计算正确的是（　　）

A、a^﹣1÷a^﹣3=a² B、（ $\frac{1}{3}$ ）⁰=0 C、（a²）³=a⁵ D、（ $\frac{1}{2}$ ）^﹣2= $\frac{1}{4}$

查看试题解析
4. 点M（3，﹣4）关于y轴的对称点的坐标是（　　）

A、（3，4） B、（﹣3，﹣4） C、（﹣3，4） D、（﹣4，3）

查看试题解析
5. 下列各式由左边到右边的变形中，是分解因式的为（　　）

A、a（x+y）=ax+ay B、x²﹣4x+4=x（x﹣4）+4 C、x²﹣16+3x=（x+4）（x﹣4）+3x D、10x²﹣5x=5x（2x﹣1）

查看试题解析
6.
如图，已知点A，D，C，F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（　　）

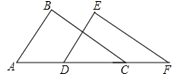A、∠BCA=∠F B、∠A=∠EDF C、BC∥EF D、∠B=∠E

查看试题解析
7. 化简 $\frac{m^{2} - 3 m}{9 - m^{2}}$ 的结果是（　　）

A、 $\frac{m}{m + 3}$ B、- $\frac{m}{m + 3}$ C、 $\frac{m}{m - 3}$ D、 $\frac{m}{3 - m}$

查看试题解析
8. AD是△BAC的角平分线，过D向AB、AC两边作垂线，垂足为E、F，则下列错误的是（　　）

A、DE=DF B、AE=AF C、BD=CD D、∠ADE=∠ADF

查看试题解析
9.
如图，∠AOB=α°，点P是∠AOB内任意一点，OP=6cm，点M和点N分别是射线OA和射线OB上的动点，若△PMN周长的最小值是6cm，则α的值是（　）

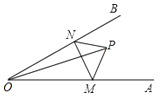A、15 B、30 C、45 D、60

查看试题解析
10. 当x分别取﹣2015、﹣2014、﹣2013、…，、﹣2、﹣1、0、1、 $\frac{1}{2}$ 、 $\frac{1}{3}$ 、…、 $\frac{1}{2013}$ 、 $\frac{1}{2014}$ 、 $\frac{1}{2015}$ 时，计算分式 $\frac{x^{2} - 1}{x^{2} + 1}$ 的值，再将所得结果相加，其和等于（　　）

A、-1 B、1 C、0 D、2015

查看试题解析

二、填空题

11. 计算4x²y•（﹣ $\frac{1}{4}$ x）= ．

查看试题解析
12. 若分式 $\frac{2 x - 4}{x + 1}$ 的值为零，则x的值为．

查看试题解析
13. 一种细菌半径是0.000 012 1米，将0.000 012 1用科学记数法表示为．

查看试题解析
14. 已知ab=2，a+b=4，则式子 $\frac{b}{a} + \frac{a}{b}$ = ．

查看试题解析
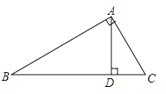
15.
如图，在△ABC中，∠BAC=90°，AD⊥BC于D，AC+CD=BD，若CD=1，则BD= ．

查看试题解析
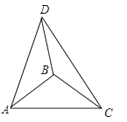
16.
如图，在△ABC中，AB=BC，∠ABC=100°，边BA绕点B顺时针旋转m°，（0＜m＜180）得到线段BD，连接AD、DC，若△ADC为等腰三角形，则m所有可能的取值是

查看试题解析

三、计算题

17. （1）计算：（12a³﹣6a²）÷3a﹣2a（2a﹣1）；
（2）解分式方程： $\frac{3}{2 x - 4}$ ﹣ $\frac{x}{x - 2}$ =1．

查看试题解析
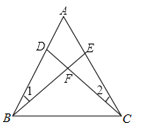
18.
如图，在△ABC中，已知∠1=∠2，BE=CD．
（1）求证：△ABE≌△ACD；
（2）请写出图中所有等腰三角形．

查看试题解析
19. 分解因式：
（1）9a﹣a³；
（2）（m+n）²﹣6m（m+n）+9m² ．

查看试题解析
20. 先化简，再求值：（1﹣ $\frac{1}{x + 2}$ ）÷ $\frac{x^{2} + 2 x + 1}{x^{2} - 4}$ ，其中x=4．

查看试题解析

四、解答题

21.
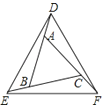
如图，已知△ABC是等边三角形，D、E、F分别是射线BA、CB、AC上一点，且AD=BE=CF，连接DE、EF、DF．
（1）求证：∠BDE=∠CEF；
（2）试判断△DEF的形状，并简要说明理由．

查看试题解析
22. 已知某项工程，乙工程队单独完成所需天数是甲工程队单独完成所需天数的两倍，若甲工程队单独做10天后，再由乙工程队单独做15天，恰好完成该工程的 $\frac{7}{10}$ ，共需施工费用85万元，甲工程队每天的施工费用比乙工程队每天的施工费用多1万元．
（1）单独完成此项工程，甲、乙两工程对各需要多少天？
（2）甲、乙两工程队每天的施工费各为多少万元？
（3）若要完成全部工程的施工费用不超过116万元，且乙工程队的施工天数大于10天，求甲工程队施工天数的取值范围？

查看试题解析
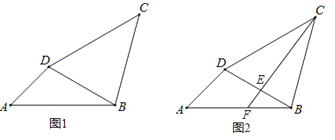
23.
如图1，在四边形ABCD中，∠CDB=2∠ABD，∠ABC=105°，∠A=∠C=45°．
（1）求∠ABD；
（2）求证：CD=AB；
（3）如图2，过点C作CF⊥BD于点E，交AB于点F，若AB=3 $\sqrt{3}$ ，则BF+BE等于多少？

查看试题解析
24.
如图1，在平面直角坐标系中，点A，B，C的坐标分别是（0，a），（b，0），（a，﹣b）且a²+b²+4a﹣4b=﹣8，连接BC交y轴于点M，N为AC中点，连接NO并延长至D，使OD=ON，连接BD．
（1）求a，b的值；
（2）求∠DBC；
（3）如图2，Q为ON，BC的交点，连接AQ，AB，过点O作OP⊥OQ，交AB于P，过点O作OH⊥AB于H，交BQ于E，请探究线段EH，PH与OH之间有何数量关系？并证明你的结论．

查看试题解析