2015-2016学年湖北省武汉市江岸区八年级上学期末数学试卷
试卷更新日期:2016-08-03 类型:期末考试
一、单选题
-
1. 下列各图中,不是轴对称图形的是( )A、
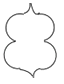 B、
B、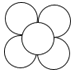 C、
C、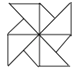 D、
D、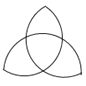 2. 给出下列式子:、、、+、9x+ , 其中,是分式的有( )A、5个 B、4个 C、3个 D、2个3. 分式有意义,则x的取值范围是( )A、x≠2 B、x≠﹣2 C、x=2 D、x=﹣24. 下列分式从左至右的变形正确的是( )A、 B、 C、 D、5. 若x+m与x+2的乘积中不含x的一次项,则m的值为( )A、2 B、1 C、0 D、-26. 下列各式可以写成完全平方式的多项式有( )A、x2+xy+y2 B、x2﹣xy+ C、x2+2xy+4y2 D、-x+17. 边长分别为a和2a的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为( )
2. 给出下列式子:、、、+、9x+ , 其中,是分式的有( )A、5个 B、4个 C、3个 D、2个3. 分式有意义,则x的取值范围是( )A、x≠2 B、x≠﹣2 C、x=2 D、x=﹣24. 下列分式从左至右的变形正确的是( )A、 B、 C、 D、5. 若x+m与x+2的乘积中不含x的一次项,则m的值为( )A、2 B、1 C、0 D、-26. 下列各式可以写成完全平方式的多项式有( )A、x2+xy+y2 B、x2﹣xy+ C、x2+2xy+4y2 D、-x+17. 边长分别为a和2a的两个正方形按如图的样式摆放并连线,则图中阴影部分的面积为( ) A、3a2 B、 C、2a2 D、8. 若xy﹣x+y=0且xy≠0,则分式的值为( )A、 B、xy C、1 D、-19. 某次列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,设提速前列车的平均速度为x千米/小时,下列方程正确的是( )
A、3a2 B、 C、2a2 D、8. 若xy﹣x+y=0且xy≠0,则分式的值为( )A、 B、xy C、1 D、-19. 某次列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,设提速前列车的平均速度为x千米/小时,下列方程正确的是( )
A、 B、x+v= C、 D、10. 如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( ) A、80° B、70° C、60° D、45°
A、80° B、70° C、60° D、45°二、填空题
-
11. (﹣2x2)2= .12. 一种病毒的直径为0.000023m,这个数用科学记数法表示为 .
13. 如果分式的值为零,则x= .
14. 若x2+2(m﹣3)x+16=(x+n)2 , 则m=15. 如图,△ABC中,AC=BC,AB=4,∠ACB=90°,以AB的中点D为圆心DC长为半径作圆DEF,设∠BDF=α(0°<α<90°),当α变化时图中阴影部分的面积为 (圆:∠EDF=90°,圆的面积=) 16. 已知△ABD≌△CDB,AD=BD,BE⊥AD于E,∠EBD=20°,则∠CDE的度数为
16. 已知△ABD≌△CDB,AD=BD,BE⊥AD于E,∠EBD=20°,则∠CDE的度数为三、计算题
-
17. 分解因式:
(1)12x2﹣3y2
(2)3ax2﹣6axy+3ay2 .
18. 解方程:
19. 求值:x2(x﹣1)﹣x(x2+x﹣1),其中x= .20.如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系.
(1)直接写出点A、B的坐标:A( ,),B( ,);
(2)请在图中确定点C(1,﹣2)的位置并连接AC、BC,则△ABC是三角形(判断其形状);
(3)在现在的网格中(包括网格的边界)存在一点P,点P的横纵坐标为整数,连接PA、PB后得到△PAB为等腰三角形,则满足条件的点P有个.

四、解答题
-
21. 若x2+y2=5,xy=2,求下列各式的值;
(1)(x+y)2(直接写出结果)
(2)x﹣y
(3)(直接写出结果)
22. 小明用a小时清点完一批图书的一半,小强加入清点另一半图书的工作,两人合作小时清点完另一半图书.设小强单独清点完这批图书需要x小时.(1)若a=3,求小强单独清点完这批图书需要的时间.
(2)请用含a的代数式表示x,并说明a满足什么条件时x的值符合实际意义.
23. 已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°、∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.
①求证:CE=AG;
②若BF=2AF,连接CF,求∠CFE的度数;
(2)如图2,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,直接写出的结果
 24. 在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.
24. 在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.(1)若a、b满足a2+b2﹣4a﹣2b+5=0.
①求a、b的值;
②如图1,在①的条件下,将点B在x轴上平移,且b满足:0<b<2;在第一象限内以AB为斜边作等腰Rt△ABC,请用b表示S四边形AOBC , 并写出解答过程.
(2)若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF.
①如图2,判断AF与BF的关系并说明理由;
②若BF=OA﹣OB,求∠OAF的度数(直接写出结果).
