2015-2016学年黑龙江省哈尔滨市双城区八年级上学期末数学试卷

试卷更新日期：2016-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算中，正确的是（　　）

A、4a﹣3a=1 B、a•a²=a³ C、3a⁶÷a³=3a² D、（ab²）²=a²b²

查看试题解析
2. 下列四个“QQ表情”图片中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在直角坐标系中，点P（2，1）关于x轴对称的点的坐标是（　　）

A、（2，1） B、（﹣2，1） C、（2，﹣1） D、（﹣2，﹣1）

查看试题解析
4. 在代数式 $\frac{1}{m}$ ， $\frac{1}{4}$ ， $\frac{2}{x + y}$ ， a+ $\frac{2 a}{3}$ 中，分式的个数是（　　）

A、2 B、3 C、4 D、5

查看试题解析
5. 已知等腰三角形两边长是8cm和4cm，那么它的周长是（　　）

A、12cm B、16cm C、16cm或20cm D、20cm

查看试题解析
6. 下列说法错误的是（　　）

A、等腰三角形的高、中线、角平分线互相重合 B、三角形两边的垂直平分线的交点到三个顶点距离相等 C、等腰三角形的两个底角相等 D、等腰三角形顶角的外角是底角的二倍

查看试题解析
7. △ABC中，AB=AC，BD平分∠ABC交AC边于点D，∠BDC=75°，则∠A的度数是（　　）

A、35° B、40° C、70° D、110°

查看试题解析
8. 某农场开挖一条长480米的渠道，开工后，每天比原计划多挖20米，结果提前4天完成任务，若设原计划每天挖x米，那么求x时所列方程正确的是（　）

A、 $\frac{480}{x} - \frac{480}{x + 20} = 4$ B、 $\frac{480}{x} - \frac{480}{x + 4} = 20$ C、 $\frac{480}{x - 20} - \frac{480}{x} = 4$ D、 $\frac{480}{x - 4} - \frac{480}{x} = 4$

查看试题解析
9. 若关于x的方程 $\frac{m - 1}{x - 1} - \frac{x}{x - 1}$ =0无解，则m的值是（　　）

A、3 B、2 C、1 D、-1

查看试题解析
10. 如图，等边三角形ABC中，D、E分别为AB、BC边上的两动点，且总使AD=BE，AE与CD交于点F，AG⊥CD于点G，则 $\frac{F G}{A F}$ =（　　）

A、 $\frac{1}{2}$ B、2 C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析

二、填空题

11. 科学家发现一种病毒的直径为0.000104米，用科学记数法表示为米．

查看试题解析
12.
如图，若△OAD≌△OBC，且∠O=65°，∠C=20°，则∠OAD=度．

查看试题解析
13. 把多项式ax²+2axy+ay²分解因式的结果是．

查看试题解析
14. 若分式 $\frac{- 6}{7 - x}$ 的值为正数，则x的取值范围．

查看试题解析
15. 当m=时，方程 $\frac{2}{m} - \frac{1}{x}$ =3的解为1．

查看试题解析
16.
如图，D是AB边上的中点，将△ABC的沿过D的直线折叠，使点A落在BC上F处，若∠B=50°，则∠ADE=度．

查看试题解析
17. 若x+ $\frac{1}{x}$ =3，则x²+ $\frac{1}{x^{2}}$ = ．

查看试题解析
18.
如图：∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF等于．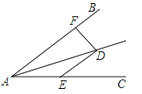

查看试题解析
19. 若（x﹣1）^x+1=1，则x= ．

查看试题解析
20.
如图，已知等边△ABC中，点D为射线BA上一点，作DE=DC，交直线BC于点E．∠ABC的平分线BF，交CD于点F，过点A作AH⊥CD于H．当∠EDC=30°，CF= $\frac{4}{3}$ ，则DH= ．

查看试题解析

三、计算题

21. （1）计算：（2x+3y）（x﹣y）
（2）计算：（3x²y﹣6xy）÷6xy．

查看试题解析
22. 先化简，再求值：（1﹣ $\frac{3}{x + 2}$ ）÷ $\frac{x^{2} - 1}{x + 2}$ ，其中x=2．

查看试题解析
23.
△ABC在平面直角坐标系中的位置如图．A、B、C三点在格点上．
（1）作出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点C₁的坐标；
（2）在y轴上找点D，使得AD+BD最小，作出点D并写出点D的坐标．

查看试题解析
24. 解下列方程
（1） $\frac{6 x}{x + 2} - 2 = 0$
（2） $\frac{3}{x - 2} = \frac{2}{x} + \frac{6}{x^{2} - 2 x}$ ．

查看试题解析

四、解答题

25.
已知：如图，Rt△ABC中，∠BAC=90°，AB=AC，D是BC的中点，AE=BF．
（1）求证：DE=DF；
（2）若BC=8，求四边形AFDE的面积．

查看试题解析
26. 动漫节开幕前，某动漫公司预测某种动漫玩具能够畅销，就分两批分别用32000元和68000元购进了这种玩具销售，其中第二批购进数量是第一批购进数量的2倍，但每套进价多了10元．
（1）该动漫公司这两批各购进多少套玩具？
（2）如果这两批玩具每套售价相同，且全部销售后总利润不少于20000元，那么每套售价至少是多少元？

查看试题解析
27.
如图，在平面直角坐标系中，点A坐标为（6，0），在B在y轴的正半轴上，且S_△AOB=24．
（1）求点B坐标；
（2）若点P从B出发沿y轴负半轴运动，速度每秒2个单位，运动时间t秒，△AOP的面积为S，求S与t的关系式，并直接写出t的取值范围；
（3）在（2）的条件下，若S_△AOP：S_△ABP=1：3，且S_△AOP+S_△ABP=S_△AOB ，在线段AB的垂直平分线上是否存在点Q，使得△AOQ的面积与△BPQ的面积相等？若存在，求出Q点坐标；若不存在，请说明理由．

查看试题解析