2015-2016学年河北省秦皇岛市卢龙县八年级上学期末数学试卷
试卷更新日期：2016-08-03 类型：期末考试
一、单选题
-
1. 已知三角形两边的长分别是5和9，则此三角形第三边的长可能是（ ）A、1 B、4 C、8 D、142. 下列图形中，轴对称图形的个数是（ ）
A、1 B、2 C、3 D、43. 下面运算正确的是（ ）A、7a2b﹣5a2b=2 B、x8÷x4=x2 C、（a﹣b）2=a2﹣b2 D、（2x2）3=8x64. 把a2﹣4a多项式分解因式，结果正确的是（ ）A、a（a﹣4） B、（a+2）（a﹣2） C、a（a+2）（a﹣2） D、（a﹣2）2﹣45. 要使分式有意义，x的取值范围满足（ ）A、x=0 B、x≠0 C、x＞0 D、x＜06. 下列各式中，计算结果是x2+7x﹣18的是（ ）A、（x﹣1）（x+18） B、（x+2）（x+9） C、（x﹣3）（x+6） D、（x﹣2）（x+9）7. 已知y2+10y+m是完全平方式，则m的值是（ ）A、25 B、±25 C、5 D、±58. 下列等式从左到右的变形，属于因式分解的是（ ）A、a（x﹣y）=ax﹣ay B、x2+2x+1=x（x+2）+1 C、（x+1）（x+3）=x2+4x+3 D、x3﹣x=x（x+1）（x﹣1）9. 如图，在△ABC中，AB=AC=20cm，DE垂直平分AB，垂足为E，交AC于D，若△DBC的周长为35cm，则BC的长为（ ）
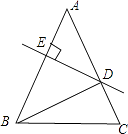A、5cm B、10cm C、15cm D、17.5cm10. 一个正多边形的每个外角都是72°，这个正多边形的边数是（ ）A、9 B、10 C、6 D、511. 下列各式中，相等关系一定成立的是（ ）A、（x﹣y）2=（y﹣x）2 B、（x+6）（x﹣6）=x2﹣6 C、（x+y）2=x2+y2 D、6（x﹣2）+x（2﹣x）=（x﹣2）（x﹣6）12.在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（ ）
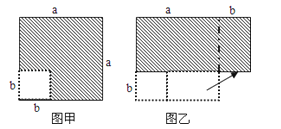A、（a+b）2=a2+2ab+b2 B、（a﹣b）2=a2﹣2ab+b2 C、a2﹣b2=（a+b）（a﹣b） D、（a+2b）（a﹣b）=a2+ab﹣2b213. 已知∠AOB=45°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1 ， O，P2三点构成的三角形是（ ）
A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形14.用大小相同的小三角形摆成如图所示的图案，按照这样的规律摆放，则第12个图案中共有小三角形的个数是（ ）
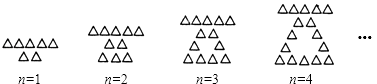A、34 B、35 C、37 D、40二、填空题
-
15. 分解因式a3﹣6a2+9a=
16. 计算：（﹣2014）0+（）﹣1﹣（﹣1）2014=17.如图，AF=DC，BC∥EF，只需补充一个条件 就得△ABC≌△DEF．
18. 禽流感病毒的形状一般为球形，直径大约为0.000000102m，该直径用科学记数法表示为m．
19. 如果分式的值为零，那么x= ．
20. 已知点A、B的坐标分别为：（2，0），（2，4），以A、B、P为顶点的三角形与△ABO全等，写出三个符合条件的点P的坐标： ．
三、计算题
-
21. 计算题：
（1）（a2）3•（a2）4÷（a2）5
（2）（x﹣y+9）（x+y﹣9）
22. 因式分解（1）﹣2a3+12a2﹣18a
（2）（x2+1）2﹣4x2 ．
四、作图题
-
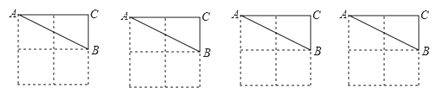
23.
如图，如下图均为2×2的正方形网格，每个小正方形的边长均为1．请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上，且位置不同的三角形．
五、解答题
