2016年河北省沧州三中中考数学模拟试卷
试卷更新日期:2016-08-01 类型:中考模拟
一、单选题
-
1. ﹣3的倒数是( )A、3 B、 C、-3 D、-2. 已知x=1是方程x2+bx﹣2=0的一个根,则方程的另一个根是( )A、1 B、2 C、-2 D、-13. 若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=1(a<b)的两个根,则实数x1 , x2 , a,b的大小关系为( )A、x1<x2<a<b B、x1<a<x2<b C、x1<a<b<x2 D、a<x1<b<x24. 二次函数y=mx2+x﹣2m(m是非0常数)的图象与x轴的交点个数为( )A、0个 B、1个 C、2个 D、1个或2个5.
某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是( )
 A、30° B、45° C、60° D、75°6. 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A、30° B、45° C、60° D、75°6. 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )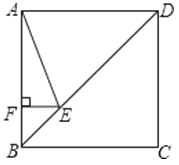 A、1 B、 C、4﹣2 D、3﹣47.
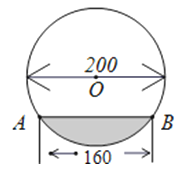
A、1 B、 C、4﹣2 D、3﹣47.在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为( )
 A、40cm B、60cm C、80cm D、100cm8.
A、40cm B、60cm C、80cm D、100cm8.如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
 A、(a﹣2,b) B、(a+2,b) C、(﹣a﹣2,﹣b) D、(a+2,﹣b)9. 甲、乙两盒中各放入分别写有数字1,2,3的三张卡片,每张卡片除数字外其他完全相同.从甲盒中随机抽出一张卡片,再从乙盒中随机摸出一张卡片,摸出的两张卡片上的数字之和是3的概率是( )A、 B、 C、 D、10. 在反比例函数y=(k<0)的图象上有两点,(﹣1,y1), (- , y2),则y1﹣y2的值是( )A、正数 B、非正数 C、负数 D、不能确定
A、(a﹣2,b) B、(a+2,b) C、(﹣a﹣2,﹣b) D、(a+2,﹣b)9. 甲、乙两盒中各放入分别写有数字1,2,3的三张卡片,每张卡片除数字外其他完全相同.从甲盒中随机抽出一张卡片,再从乙盒中随机摸出一张卡片,摸出的两张卡片上的数字之和是3的概率是( )A、 B、 C、 D、10. 在反比例函数y=(k<0)的图象上有两点,(﹣1,y1), (- , y2),则y1﹣y2的值是( )A、正数 B、非正数 C、负数 D、不能确定二、填空题
-
11. 如图,二次函数y=x2﹣6x+5的图象交x轴于A、B两点,交y轴于点C,则△ABC的面积为 .
 12. 若关于x的二次方程(m2﹣2)x2﹣(m﹣2)x+1=0的两实根互为倒数,则m= .13.
12. 若关于x的二次方程(m2﹣2)x2﹣(m﹣2)x+1=0的两实根互为倒数,则m= .13.如图,a∥b,∠1=40°,∠2=80°,则∠3= 度.
 14. 如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为 .
14. 如图,在矩形ABCD中,AB=8,AD=6,P,Q分别是AB和CD上的任意一点,且AP=CQ,线段EF是PQ的垂直平分线,交BC于F,交PQ于E.设AP=x,BF=y,则y与x的函数关系式为 . 15. 从﹣3、1、﹣2这三个数中任取两个不同的数,积为正数的概率是 .16.
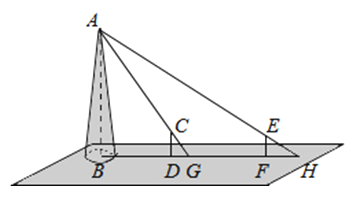
15. 从﹣3、1、﹣2这三个数中任取两个不同的数,积为正数的概率是 .16.如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是 米.
 17. 如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4 , AC=5,AD=4,则⊙O的直径AE= .
17. 如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4 , AC=5,AD=4,则⊙O的直径AE= . 18.
18.如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α= 度.

三、解答题
-
19. 先化简,再求值:(+)•(x2﹣1),其中x= .20. 某班组织班团活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品,已知笔记本2元/本,中性笔1元/支,且每种奖品至少买1件.
(1)若设购买笔记本x本,中性笔y支,写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
(3)从上述方案中任选一种方案购买,求买到的中性笔与笔记本数量相等的概率.
21.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
 22. 某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:
22. 某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.
23. 如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.