浙江省宁波市鄞州区2017-2018学年九年级上学期数学第一次阶段性检测试卷
试卷更新日期:2017-11-02 类型:月考试卷
一、选择题
-
1. 抛物线 的对称轴是直线( )
A、 B、 C、 D、2. ⊙O的半径为3cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是( )A、点A在圆内 B、点A在圆上 C、点A在圆外 D、不能确定3. 下列说法错误的是( )A、同时抛两枚普通正方体骰子,点数都是4的概率为 B、不可能事件发生机会为0 C、买一张彩票会中奖是可能事件 D、一件事发生机会为1.0%,这件事就有可能发生4. 如图,A、B、C是⊙O上的三点,已知 ,则 ( )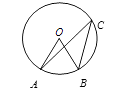 A、15° B、 C、 D、5. 如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A、15° B、 C、 D、5. 如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A、 B、
B、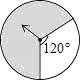 C、
C、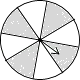 D、
D、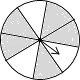 6. 如果两个相似多边形面积的比为1:5,则它们的相似比为( )
6. 如果两个相似多边形面积的比为1:5,则它们的相似比为( )
A、1:25 B、1:5 C、1:2.5 D、1:7. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )来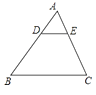 A、
A、 B、
B、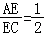 C、
C、 D、
D、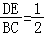 8. 如图,点D在 的边AC上,要判断 与 相似,添加一个条件,不正确的是( )
8. 如图,点D在 的边AC上,要判断 与 相似,添加一个条件,不正确的是( ) A、 B、 C、 D、9. 如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0).下列结论中,正确的一项是( )
A、 B、 C、 D、9. 如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0).下列结论中,正确的一项是( ) A、 <0 B、 <0 C、 <0 D、4ac−b2010. 如图,△ABC是 的内接等边三角形,AB=1.点D , E在圆上,四边形 为矩形,则这个矩形的面积是( )
A、 <0 B、 <0 C、 <0 D、4ac−b2010. 如图,△ABC是 的内接等边三角形,AB=1.点D , E在圆上,四边形 为矩形,则这个矩形的面积是( )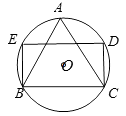 A、 B、 C、 D、111. 已知,如图,点C、D在⊙O上,直径AB=6 ,弦AC、BD相交于点E . 若CE=BC , 则阴影部分面积为( )
A、 B、 C、 D、111. 已知,如图,点C、D在⊙O上,直径AB=6 ,弦AC、BD相交于点E . 若CE=BC , 则阴影部分面积为( )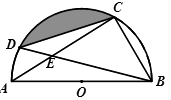 A、 B、 C、 D、12. 如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A、 B、 C、 D、12. 如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( ) A、
A、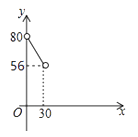 B、
B、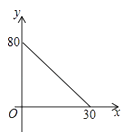 C、
C、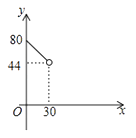 D、
D、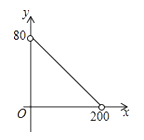
二、填空题
-
13. 若 ,则 的值为 .14. 将抛物线y=x²+1的图像先向左平移2个单位,再向下平移3个单位,所得抛物线的解析式是 .
15. 如图,△ABC的顶点坐标分别为A(0,3),B(2,1),C(2,-3),则△ABC的外心坐标是 .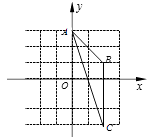 16. 在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,若AE=2,△ADE的面积为4,四边形BCED的面积为5,则边AB的长为 .
16. 在△ABC中,点D、E分别在AB、AC上,∠AED=∠B,若AE=2,△ADE的面积为4,四边形BCED的面积为5,则边AB的长为 .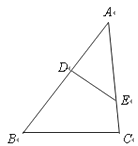 17. 如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°得到点F,则线段AF的长的最小值 .
17. 如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°得到点F,则线段AF的长的最小值 . 18. 如图,已知抛物线y=mx2﹣6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥ x轴,交该抛物线于M、N两点,交⊙ P与E、F两点,若EF=2 ,则MN的长是 .
18. 如图,已知抛物线y=mx2﹣6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥ x轴,交该抛物线于M、N两点,交⊙ P与E、F两点,若EF=2 ,则MN的长是 .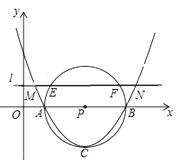
三、解答题
-
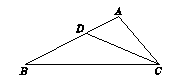
19. 如图所示,点D在△ABC的AB边上,AD=1,BD=2,AC= .求证:△ACD∽△ABC.
 20. 已知一个口袋中装有4个只有颜色不同的球,其中3个白球,1个黑球.
20. 已知一个口袋中装有4个只有颜色不同的球,其中3个白球,1个黑球.
(1)、求从中随机抽取出一个黑球的概率是多少;
(2)、若从口袋中摸出一个球,记下颜色后不放回,再摸出一个球。请列表或作出树状图,求两次都摸出白球的概率.
21. 正方形网格中,小格的顶点叫做格点.三个顶点都在网格上的三角形叫做格点三角形.小华已在左边的正方形网格中作出了格点△ABC.请你在右边的两个正方形网格中各画出一个不同的格点三角形,使得三个网格中的格点三角形都相似(不包括全等).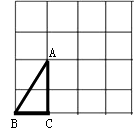
 22. 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
22. 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D. (1)、请直接写出D点的坐标;(2)、求二次函数的解析式;(3)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
(1)、请直接写出D点的坐标;(2)、求二次函数的解析式;(3)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
23. 在△ABC中,AB=AC= , BC=2,以AB为直径的⊙O分别交AC、BC于点D、E。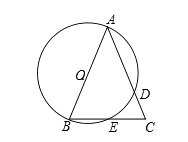 (1)、求证:E是BC的中点;(2)、连结DE,求证:△CDE∽△CBA;(3)、求△CDE的面积.
(1)、求证:E是BC的中点;(2)、连结DE,求证:△CDE∽△CBA;(3)、求△CDE的面积.
24. 如图,直线 与x轴交于点A,与直线 y=kx-3交于点C(c,6),直线 与y轴交于点B,连接AB. (1)、求k的值;(2)、求证:∠CAO=∠BAO;(3)、P为OA上一点,连结PB,M为PB中点,延长MO交直线AC于点N,若OP=x, ,求y关于x的函数表达式.
(1)、求k的值;(2)、求证:∠CAO=∠BAO;(3)、P为OA上一点,连结PB,M为PB中点,延长MO交直线AC于点N,若OP=x, ,求y关于x的函数表达式.
25. 抛物线C:y=x2+bx+c 交 轴于点A(0,-1)且过点 , P是抛物线C上一个动点,过P作PB∥OA,以P为圆心,2为半径的圆交PB于C、D两点(点D位于点C下方).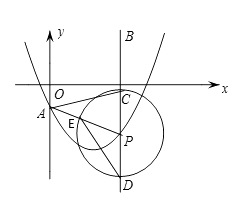 (1)、求抛物线C的解析式;(2)、连接AP交⊙P于点E,连接DE,AC.若ΔACP是以CP为直角边的直角三角形,求∠EDC的度数;(3)、若当点P经过抛物线C上所有的点后,点D随之经过的路线被直线 截得的线段长为8,求 的值.
(1)、求抛物线C的解析式;(2)、连接AP交⊙P于点E,连接DE,AC.若ΔACP是以CP为直角边的直角三角形,求∠EDC的度数;(3)、若当点P经过抛物线C上所有的点后,点D随之经过的路线被直线 截得的线段长为8,求 的值.
26. 我们知道:有一内角为直角的三角形叫做直角三角形.类似地,我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(-4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A,B,D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然△DCE,△DEF,△DAE是半直角三角形.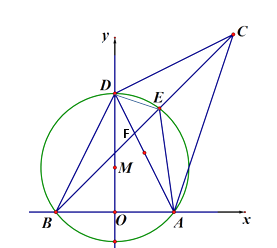 (1)、求证:△ABC是半直角三角形;(2)、求证:∠DEC=∠DEA;(3)、若点D的坐标为(0,8),
(1)、求证:△ABC是半直角三角形;(2)、求证:∠DEC=∠DEA;(3)、若点D的坐标为(0,8),①求AE的长;
②记BC与AD的交点为F,求ΔACF与ΔBCA的面积之比.