2016年山东省泰安市新泰市中考数学模拟试卷(四)
试卷更新日期:2016-07-29 类型:中考模拟
一、单选题
-
1. 比1小2的数是( )A、-1 B、-2 C、-3 D、12. 下列运算正确的是( )A、=±3 B、|﹣3|=﹣3 C、﹣=﹣3 D、﹣32=93. 在平面直角坐标系中,点P的坐标为(﹣2,a2+1),则点P所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知空气的单位体积质量为1.24×10﹣3克/厘米3 , 1.24×10﹣3用小数表示为( )A、0.000124 B、0.0124 C、﹣0.00124 D、0.001245. 若2x=3,4y=5.则2x﹣2y的值为( )A、 B、-2 C、 D、6.
骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两对面上所写的两个数字之和为7.将这样相同的几个骰子按照相接触的两个面上的数字的积为6摆成一个几何体,这个几何体的三视图如图所示.已知图中所标注的是部分面上的数字,则“*”所代表的数是( )
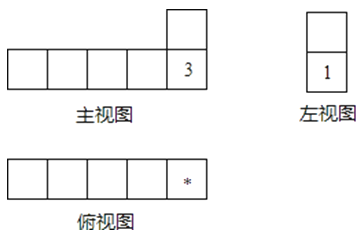 A、2 B、4 C、5 D、67.
A、2 B、4 C、5 D、67.观察标志,从图案看既是轴对称图形又是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个8. 已知关于x的不等式组 只有四个整数解,则实数a的取值范围是( )A、﹣3<a<﹣2 B、﹣3≤a≤﹣2 C、﹣3≤a<﹣2 D、﹣3<a≤﹣29. 如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
A、1个 B、2个 C、3个 D、4个8. 已知关于x的不等式组 只有四个整数解,则实数a的取值范围是( )A、﹣3<a<﹣2 B、﹣3≤a≤﹣2 C、﹣3≤a<﹣2 D、﹣3<a≤﹣29. 如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )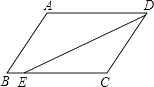 A、2cm B、4cm C、6cm D、8cm10.
A、2cm B、4cm C、6cm D、8cm10.如图,将Rt△ABC(其中∠B=34°,∠C=90°)绕A点按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角最小等于( )
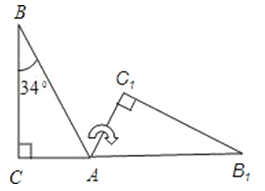 A、56° B、68° C、124° D、180°11. 若关于x的分式方程 无解,则m的值为( )A、﹣1.5 B、1 C、﹣1.5或2 D、﹣0.5或﹣1.512. 已知二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象大致是( )
A、56° B、68° C、124° D、180°11. 若关于x的分式方程 无解,则m的值为( )A、﹣1.5 B、1 C、﹣1.5或2 D、﹣0.5或﹣1.512. 已知二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象大致是( )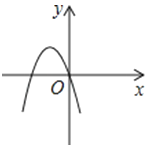 A、
A、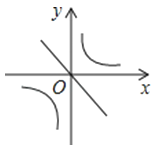 B、
B、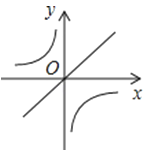 C、
C、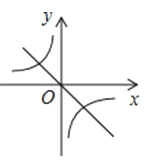 D、
D、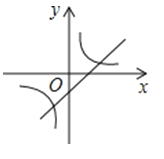 13. 要得到二次函数y=﹣x2+2x﹣2的图象,需将y=﹣x2的图象( )A、向左平移2个单位,再向下平移2个单位 B、向右平移2个单位,再向上平移2个单位 C、向左平移1个单位,再向上平移1个单位 D、向右平移1个单位,再向下平移1个单位14. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
13. 要得到二次函数y=﹣x2+2x﹣2的图象,需将y=﹣x2的图象( )A、向左平移2个单位,再向下平移2个单位 B、向右平移2个单位,再向上平移2个单位 C、向左平移1个单位,再向上平移1个单位 D、向右平移1个单位,再向下平移1个单位14. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( ) A、(6+)米 B、12米 C、(4﹣2)米 D、10米15. 在反比例函数 y=(k<0)的图象上有两点(﹣1,y1),(- , y2),则y1﹣y2的值是( )A、负数 B、非正数 C、正数 D、不能确定16.
A、(6+)米 B、12米 C、(4﹣2)米 D、10米15. 在反比例函数 y=(k<0)的图象上有两点(﹣1,y1),(- , y2),则y1﹣y2的值是( )A、负数 B、非正数 C、正数 D、不能确定16.如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是( )
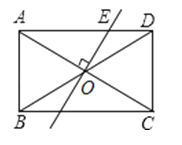 A、1.6 B、2.5 C、3 D、3.417. 关于x、y的方程组 的解是 , 则|m﹣n|的值是( )A、5 B、3 C、2 D、118. 如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为( )
A、1.6 B、2.5 C、3 D、3.417. 关于x、y的方程组 的解是 , 则|m﹣n|的值是( )A、5 B、3 C、2 D、118. 如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为( )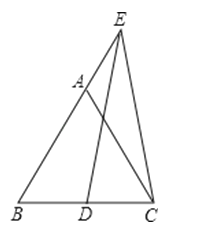 A、2 B、3 C、 D、+119.
A、2 B、3 C、 D、+119.如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C﹣D﹣E上移动,若点C,D,E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
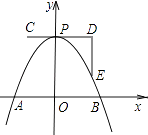 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
20. 分解因式:2x2﹣12x+18= .21. 如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则FG:AF= .
 22. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
22. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 . 23.
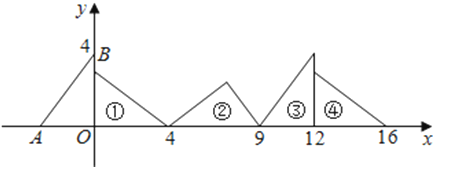
23.如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④…,则三角形⑩的直角顶点的坐标为 .
三、解答题
-
24. 近年来,地震、泥石流等自然灾害频繁发生,造成极大的生命和财产损失.为了更好地做好“防震减灾”工作,我市相关部门对某中学学生“防震减灾”的知晓率采取随机抽样的方法进行问卷调查,调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级.小明根据调查结果绘制了如下统计图,请根据提供的信息回答问题:
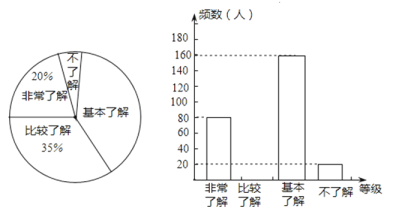
(1)本次参与问卷调查的学生有多少人;扇形统计图中“基本了解”部分所对应的扇形圆心角是多少度;在该校2000名学生中随机提问一名学生,对“防震减灾”不了解的概率为多少.
(2)请补全频数分布直方图.
25. 我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
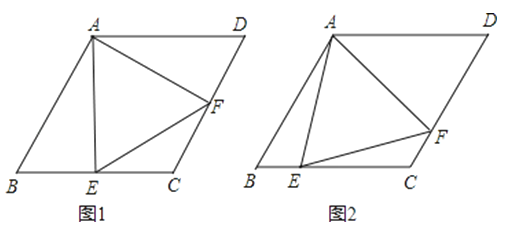
26. 菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
 27.
27.某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植﹣亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.
