2017-2018学年人教版九年级上学期数学期中模拟试卷
试卷更新日期:2017-10-31 类型:期中考试
一、单选题
-
1. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、
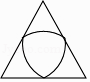 B、
B、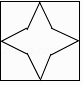 C、
C、 D、
D、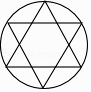 2. 已知关于x的方程x2+x﹣a=0的一个根为2,则另一个根是( )A、﹣3 B、﹣2 C、3 D、63. 抛物线 (m是常数)的顶点在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 方程x 2﹣5x=0的解是( )A、x1=0,x2=﹣5 B、x=5 C、x1=0,x2=5 D、x=05. 抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是( ).
2. 已知关于x的方程x2+x﹣a=0的一个根为2,则另一个根是( )A、﹣3 B、﹣2 C、3 D、63. 抛物线 (m是常数)的顶点在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 方程x 2﹣5x=0的解是( )A、x1=0,x2=﹣5 B、x=5 C、x1=0,x2=5 D、x=05. 抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是( ).x
…
-4
-3
-2
-1
0
1
…
y
…
-37
-21
-9
-1
3
3
…
A、当x>1时y随x的增大而增大 B、抛物线的对称轴为x= C、当x=2时y=-1 D、方程ax2+bx+c=0一个负数解x1满足-1<x1<06. 心理学家发现:学生对概念的接受能力y与提出概念的时间x(min)之间是二次函数关系,当提出概念13min时,学生对概念的接受力最大,为59.9;当提出概念30min时,学生对概念的接受能力就剩下31,则y与x满足的二次函数关系式为( )A、y=﹣(x﹣13)2+59.9 B、y=﹣0.1x2+2.6x+31 C、y=0.1x2﹣2.6x+76.8 D、y=﹣0.1x2+2.6x+437. 若关于x的一元二次方程(k+1)x2+2(k+1)x+k﹣2=0有实数根,则k的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、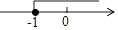 D、
D、 8.
8.如图,若将△ABC绕点O逆时针旋转90°,则顶点B的对应点B1的坐标为( )
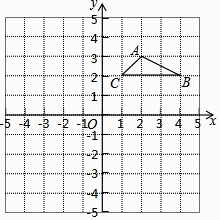 A、(﹣4,2) B、(﹣2,4) C、(4,﹣2) D、(2,﹣4)9. 若x1 , x2是方程x2﹣2mx+m2﹣m﹣1=0的两个根,且x1+x2=1﹣x1x2 , 则m的值为( )A、﹣1或2 B、1或﹣2 C、﹣2 D、110. 若一次函数y=(a+1)x+a的图象过第一、三、四象限,则二次函数y=ax2﹣ax( )A、有最大值 B、有最大值﹣ C、有最小值 D、有最小值﹣
A、(﹣4,2) B、(﹣2,4) C、(4,﹣2) D、(2,﹣4)9. 若x1 , x2是方程x2﹣2mx+m2﹣m﹣1=0的两个根,且x1+x2=1﹣x1x2 , 则m的值为( )A、﹣1或2 B、1或﹣2 C、﹣2 D、110. 若一次函数y=(a+1)x+a的图象过第一、三、四象限,则二次函数y=ax2﹣ax( )A、有最大值 B、有最大值﹣ C、有最小值 D、有最小值﹣二、填空题
-
11. 若实数a、b满足 ,则 .
12. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD=度. 13. 当m=时,关于x的方程(m+2)x|m﹣1|﹣1+2mx+3=0是一元二次方程.14. 已知方程x2+5x+1=0的两个实数根分别为x1、x2 , 则x12+x22= .15.
13. 当m=时,关于x的方程(m+2)x|m﹣1|﹣1+2mx+3=0是一元二次方程.14. 已知方程x2+5x+1=0的两个实数根分别为x1、x2 , 则x12+x22= .15.如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 .
 16. 已知关于x的方程x2﹣3x+m=0的一个根是2,则它的另一个根是 , m的值是 .17. 若x2+2x与2x+3互为相反数,则x= .18. 如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2= (x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是(填写正确结论的序号).
16. 已知关于x的方程x2﹣3x+m=0的一个根是2,则它的另一个根是 , m的值是 .17. 若x2+2x与2x+3互为相反数,则x= .18. 如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2= (x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是(填写正确结论的序号).
三、作图题
-
19. 在4×4的方格内选5个小正方形,让它们组成一个轴对称图形,请在图中画出你的4种方案.(每个4×4的方格内限画一种)
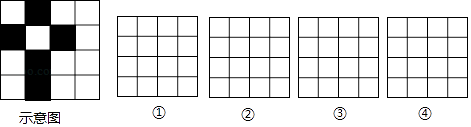
要求:
①5个小正方形必须相连(有公共边或公共顶点式为相连)
②将选中的小正方行方格用黑色签字笔涂成阴影图形.(每画对一种方案得2分,若两个方案的图形经过反折、平移、旋转后能够重合,均视为一种方案)
四、综合题
-
20. 在等腰△ABC中,三边分别为a、b、c,其中 ,若关于x的方程 有两个相等的实数根,求△ABC的周长.21.
图中是抛物线形拱桥,当水面宽AB=8米时,拱顶到水面的距离CD=4米.如果水面上升1米,那么水面宽度为多少米?

 22. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
22. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.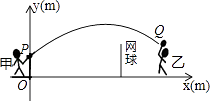 (1)、当a=﹣ 时,
(1)、当a=﹣ 时,①求h的值;
②通过计算判断此球能否过网.
(2)、若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 m的Q处时,乙扣球成功,求a的值.23. 已知关于x的一元二次方程x2﹣(m+1)x+ (m2+1)=0有实数根.(1)、求m的值;(2)、先作y=x2﹣(m+1)x+ (m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;(3)、在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2﹣4n的最大值和最小值.24. 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB. (1)、求点P与点Q之间的距离;(2)、求∠APB的度数.25. 某公司生产一种新型生物医药产品,生产成本为2万元/ 吨,每月生产能力为12吨,且生产出的产品都能销售出去.这种产品部分内销,另一部分外销(出口),内销与外销的单价 (单位:万元/吨)与销量的关系分别如图1,图2.
(1)、求点P与点Q之间的距离;(2)、求∠APB的度数.25. 某公司生产一种新型生物医药产品,生产成本为2万元/ 吨,每月生产能力为12吨,且生产出的产品都能销售出去.这种产品部分内销,另一部分外销(出口),内销与外销的单价 (单位:万元/吨)与销量的关系分别如图1,图2.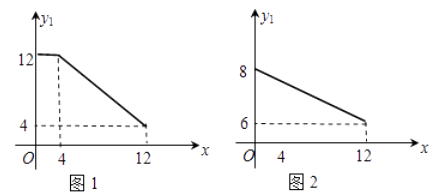 (1)、如果该公司内销数量为x(单位:吨),内、外销单价分别为y 1 , y 2 ,求, 关于x的函数解析式;(2)、如果该公司内销数量为x(单位:吨),求内销获得的毛利润 关于x的函数解析式;(3)、请设计一种销售方案,使该公司本月能获得最大毛利润,并求出毛利润的最大值.(毛利润=销售收入-生产成本).
(1)、如果该公司内销数量为x(单位:吨),内、外销单价分别为y 1 , y 2 ,求, 关于x的函数解析式;(2)、如果该公司内销数量为x(单位:吨),求内销获得的毛利润 关于x的函数解析式;(3)、请设计一种销售方案,使该公司本月能获得最大毛利润,并求出毛利润的最大值.(毛利润=销售收入-生产成本).
26.如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
 (1)、求点B,C的坐标;(2)、判断△CDB的形状并说明理由;(3)、将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
(1)、求点B,C的坐标;(2)、判断△CDB的形状并说明理由;(3)、将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
-