2017-2018学年浙教版九年级上学期数学期中模拟试卷

试卷更新日期：2017-10-30 类型：期中考试

进入出卷网下载

一、单选题

1. 在落实“小组合作学习，当堂达标检测及评价”要求中，某班四个小组设计的组徽图案如图，这四个图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 二次函数 $y = a x^{2} - 4 x + 1$ 有最小值 $- 3$ ，则 a的值为（）

A、1 B、-1 C、 $\pm 1$ D、 $\frac{1}{2}$

查看试题解析
3. 如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD长（）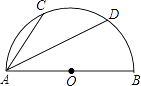

A、4 $\sqrt{5}$ cm B、3 $\sqrt{5}$ cm C、5 $\sqrt{5}$ cm D、4 cm

查看试题解析
4. 已知抛物线y=x²﹣2mx﹣4（m＞0）的顶点M关于坐标原点O的对称点为M′，若点M′在这条抛物线上，则点M的坐标为（）

A、（1，﹣5） B、（3，﹣13） C、（2，﹣8） D、（4，﹣20）

查看试题解析
5. 二次函数y=ax²+bx+c的图象如图所示，以下结论：①abc＞0；②4ac＜b²；③2a+b＞0；④其顶点坐标为（ $\frac{1}{2}$ ，﹣2）；⑤当x＜ $\frac{1}{2}$ 时，y随x的增大而减小；⑥a+b+c＞0正确的有（）

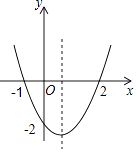A、3个 B、4个 C、5个 D、6个

查看试题解析
6. 如图，D是等边△ABC外接圆上的点，且∠DAC=20°，则∠ACD的度数为（）

A、20° B、30° C、40° D、45°

查看试题解析
7. 矩形ABCD的两条对称轴为坐标轴，点A的坐标为（2，1）.一张透明纸上画有一个点和一条抛物线，平移透明纸，这个点与点A重合，此时抛物线的函数表达式为y=x² ，再次平移透明纸，使这个点与点C重合，则该抛物线的函数表达式变为（）

A、y=x²+8x+14 B、y=x²-8x+14 C、y=x²+4x+3 D、y=x²-4x+3

查看试题解析
8. 如图，在3×3的正方形网格图中，有3个小正方形涂成了黑色，现在从白色小正方形中任意选取一个并涂成黑色，使黑色部分的图形构成一个轴对称图形的概率是（）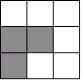

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
9. 一条弦分圆周为5：7，这条弦所对的圆周角为（）

A、75° B、105° C、60°或120° D、75°或105°

查看试题解析
10. 圆内接四边形ABCD中，∠A，∠B，∠C的度数的比为2：3：6，∠D的度数为（　　）

A、45° B、67.5° C、135° D、112.5°

查看试题解析

二、填空题

11. 任取不等式组 ${\begin{matrix} k - 3 \leq 0 \\ 2 k + 5 > 0 \end{matrix}$ 的一个整数解，则能使关于x的方程：2x+k=﹣1的解为非负数的概率为．

查看试题解析
12. 经过A（4，0），B（﹣2，0），C（0，3）三点的抛物线解析式是．

查看试题解析
13. 如图，点P（3，4），⊙P半径为2，A（2.8，0），B（5.6，0），点M是⊙P上的动点，点C是MB的中点，则AC的最小值是．

查看试题解析
14. 如图，将弧AC沿弦AC折叠交直径AB于圆心O，则弧AC=度．

查看试题解析
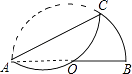15. 二次函数y=ax²+bx+c和一次函数y=mx+n的图象如图所示，则ax²+bx+c≤mx+n时，x的取值范围是．

查看试题解析
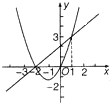16.
如图，AB是⊙O的直径CD是弦，若AB=10cm，CD=8cm，那么A、B两点到直线CD的距离之和为 cm.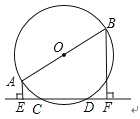

查看试题解析

三、综合题

17. 已知二次函数 $y = x^{2} - 4 x + 3$ .
（1）求顶点坐标和对称轴方程；
（2）求该函数图象与x标轴的交点坐标；
（3）指出x为何值时， $y > 0$ ；当x为何值时， $y < 0$ .

查看试题解析
18. 夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务，为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元．

(1)、设第x天生产空调y台，直接写出y与x之间的函数解析式，并写出自变量x的取值范围．

(2)、若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第x天的利润为W元，试求W与x之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少．

查看试题解析
19. 如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，弧AE等于弧AB，BE分别交AD、AC于点F、G．

(1)、判断△FAG的形状，并说明理由；

(2)、若点E和点A在BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，（1）中的结论还成立吗？请说明理由．

查看试题解析
20. 某班有50位学生，每位学生都有一个序号，将50张编有学生序号（从1号到50号）的卡片（除序号不同外其它均相同）打乱顺序重新排列，从中任意抽取1张卡片．

(1)、在序号中，是20的倍数的有：20，40，能整除20的有：1，2，4，5，10（为了不重复计数，20只计一次），求取到的卡片上序号是20的倍数或能整除20的概率；

(2)、若规定：取到的卡片上序号是k（k是满足1≤k≤50的整数），则序号是k的倍数或能整除k（不重复计数）的学生能参加某项活动，这一规定是否公平？请说明理由；

(3)、请你设计一个规定，能公平地选出10位学生参加某项活动，并说明你的规定是符合要求的．

查看试题解析
21. 如图，将线段AB绕点A逆时针旋转60°得AC，连接BC，作△ABC的外接圆⊙O，点P为劣弧 $\hat{A B}$ 上的一个动点，弦AB，CP相交于点D．

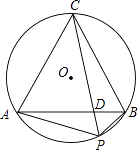(1)、求∠APB的大小；

(2)、当点P运动到何处时，PD⊥AB？并求此时CD：CP的值；

(3)、在点P运动过程中，比较PC与AP+PB的大小关系，并对结论给予证明．

查看试题解析
22. 交通工程学理论把在单向道路上行驶的汽车看成连续的液体，并用流量、速度、密度三个概念描述车流的基本特征。其中流量q（辆/小时）指单位时间内通过道路指定断面的车辆数；速度v（千米/小时）指通过道路指定断面的车辆速度；密度（辆/千米）指通过道路指定断面单位长度内的车辆数，为配合大数据治堵行动，测得某路段流量q与速度v之间的部分数据如下表：
速度v（千米/小时）
…
5
10
20
32
40
48
…
流量q（辆/小时）
…
550
1000
1600
1792
1600
1152
…

(1)、根据上表信息，下列三个函数关系式中，刻画q，v关系最准确的是（只需填上正确答案的序号）① $q = 90 v + 100$ ② $q = \frac{32000}{v}$ ③ $q = - 2 v^{2} + 120 v$

(2)、请利用（1）中选取的函数关系式分析，当该路段的车流速为多少时，流量达到最大？最大流量是多少？

(3)、已知q，v，k满足 $q = v k$ ，请结合（1）中选取的函数关系式继续解决下列问题：
①市交通运行监控平台显示，当 $12 \leq v < 18$ 时道路出现轻度拥堵，试分析当车流密度k在什么范围时，该路段出现轻度拥堵；
②在理想状态下，假设前后两车车头之间的距离d（米）均相等，求流量q最大时d的值

查看试题解析
23. 抛物线y=4x²﹣2ax+b与x轴相交于A（x₁ ， 0），B（x₂ ， 0）（0＜x₁＜x₂）两点，与y轴交于点C．

(1)、设AB=2，tan∠ABC=4，求该抛物线的解析式；

(2)、在（1）中，若点D为直线BC下方抛物线上一动点，当△BCD的面积最大时，求点D的坐标；

(3)、是否存在整数a，b使得1＜x₁＜2和1＜x₂＜2同时成立，请证明你的结论．

查看试题解析

速度v（千米/小时）	…	5	10	20	32	40	48	…
流量q（辆/小时）	…	550	1000	1600	1792	1600	1152	…