2017-2018学年人教版八年级上学期数学期中模拟试卷
试卷更新日期:2017-10-30 类型:期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若等腰三角形的两边长分别4和6,则它的周长是( )
2. 若等腰三角形的两边长分别4和6,则它的周长是( )
A、14 B、15 C、16 D、14或163. 有一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )A、△ABC三条角平分线的交点 B、△ABC三边的垂直平分线的交点 C、△ABC三条中线的交点 D、△ABC三条高所在直线的交点4. 已知点P(a+1,2a﹣1)关于x轴的对称点在第一象限,则a的取值范围是( )A、a>﹣1 B、a< C、﹣1 D、﹣15. 如图,已知AE=CF,∠AFD=∠CEB,那么添加一个条件后,仍无法判定△ADF≌△CBE的是( ) A、AD=CB B、∠A=∠C C、BE=DF D、AD∥BC6. 下列说法正确的是( )A、轴对称是两个图,轴对称图形是一个图 B、若两线段互相垂直平分,则这两线段互为对称轴 C、所有直角三角形都不是轴对称图形 D、两个内角相等的三角形不是轴对称图7. 如图,AD是△ABC的边BC上的中线,BE是△ABD的边AD上的中线,若△ABC的面积是16,则△ABE的面积是( )
A、AD=CB B、∠A=∠C C、BE=DF D、AD∥BC6. 下列说法正确的是( )A、轴对称是两个图,轴对称图形是一个图 B、若两线段互相垂直平分,则这两线段互为对称轴 C、所有直角三角形都不是轴对称图形 D、两个内角相等的三角形不是轴对称图7. 如图,AD是△ABC的边BC上的中线,BE是△ABD的边AD上的中线,若△ABC的面积是16,则△ABE的面积是( )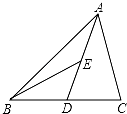 A、16 B、8 C、4 D、28. 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A、16 B、8 C、4 D、28. 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )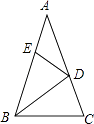 A、2个 B、3个 C、4个 D、5个9. 如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( )
A、2个 B、3个 C、4个 D、5个9. 如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) A、1个 B、2个 C、3个 D、4个10. 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
A、1个 B、2个 C、3个 D、4个10. 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )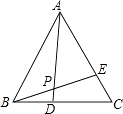 A、45° B、55° C、60° D、75°
A、45° B、55° C、60° D、75°二、填空题
-
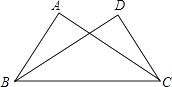
11. 已知点P(3,a)关于y轴的对称点为Q(b,2),则ab= .12. 如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是 .
 13. 如图,在△ABC中,∠C=90°,AM是∠BAC的平分线,CM=20cm,那么M到AB的距离为
13. 如图,在△ABC中,∠C=90°,AM是∠BAC的平分线,CM=20cm,那么M到AB的距离为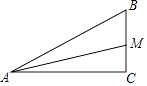 14. 如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= .
14. 如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= .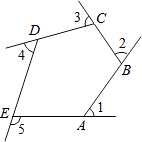 15. 如图,在△ABC中,AB=7cm,AC=4cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为 cm.
15. 如图,在△ABC中,AB=7cm,AC=4cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为 cm.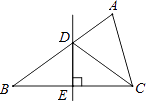 16. 一个多边形的每一个外角都等于36°,则该多边形的内角和等于度.17. 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是 .
16. 一个多边形的每一个外角都等于36°,则该多边形的内角和等于度.17. 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是 .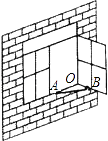 18. 如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为 .
18. 如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为 .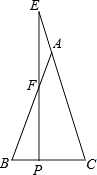 19. 如图,小亮从A点出发前10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了 m.
19. 如图,小亮从A点出发前10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了 m.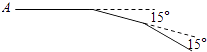 20. 如图:△ABE≌△ACD,AB=10cm,∠A=60°,∠B=30°,则AD=cm,∠ADC= .
20. 如图:△ABE≌△ACD,AB=10cm,∠A=60°,∠B=30°,则AD=cm,∠ADC= .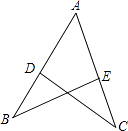
三、作图题
-
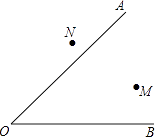
21. 已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法).
四、解答题
-
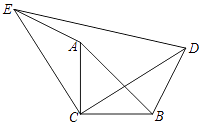
22. 如图,△ABC和△CDE都是等腰直角三角形,且CA=CB,CE=CD.求证:△ACE≌△BCD.
 23. 在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.24. 已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:D在∠BAC的平分线上.
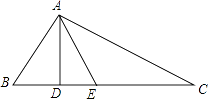
23. 在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.24. 已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:D在∠BAC的平分线上.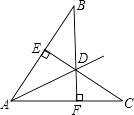 25. 如图,在△ABC中,AD是高,在线段DC上取一点E,使DE=BD,已知AB+BD=DC.
25. 如图,在△ABC中,AD是高,在线段DC上取一点E,使DE=BD,已知AB+BD=DC.求证:E点在线段AC的垂直平分线上.
五、综合题
-
26. 已知:如图,△ABC和△DBE均为等腰直角三角形.
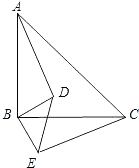 (1)、求证:AD=CE;(2)、猜想:AD和CE是否垂直?若垂直,请说明理由;若不垂直,则只要写出结论,不用写理由.27. 在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)、求证:AD=CE;(2)、猜想:AD和CE是否垂直?若垂直,请说明理由;若不垂直,则只要写出结论,不用写理由.27. 在边长为1的小正方形网格中,△AOB的顶点均在格点上,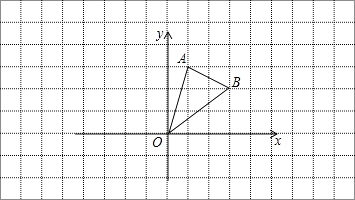 (1)、B点关于y轴的对称点坐标为;(2)、将△AOB向左平移3个单位长度得到△A1O1B1 , 请画出△A1O1B1;(3)、在(2)的条件下,A1的坐标为 .28. 阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
(1)、B点关于y轴的对称点坐标为;(2)、将△AOB向左平移3个单位长度得到△A1O1B1 , 请画出△A1O1B1;(3)、在(2)的条件下,A1的坐标为 .28. 阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究一:如图1,在△ABC中,已知O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+ ∠A,理由如下:
∵BO和CO分别是∠ABC与∠ACB的平分线,
∴∠1= ∠ABC,∠2= ∠ACB;
∴∠1+∠2= (∠ABC+∠ACB)= (180°﹣∠A)=90°﹣ ∠A,
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣ ∠A)=90°+ ∠A.
 (1)、探究二:如图2中,已知O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?并说明理由.(2)、探究二:如图3中,已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?
(1)、探究二:如图2中,已知O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?并说明理由.(2)、探究二:如图3中,已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?
-