四川省眉山市东坡区2021届九年级下学期数学开学试卷
试卷更新日期:2021-04-02 类型:开学考试
一、选择题 (每题3分,共36分)
-
1. 要使代数式 有意义,则x的取值范围是( )A、x>﹣1 B、x≥﹣1 C、x≠0 D、x>﹣1且x≠02. 下列四组线段中,是成比例线段的是( )A、2cm,3cm,4cm,5cm B、3cm,6cm,0.2dm,5cm C、2cm,4cm,6cm,8cm D、12cm,8cm,15cm,10cm3. 化简后的结果为( )A、 B、 C、 D、4. 关于x的一元二次方程x2﹣(k+2)x+2k=0的根的情况是( )A、有两个不相等的实数根 B、总有实数根 C、有两个相等的实数根 D、没有实数根5. 如图,已知△ACD∽△ADB,AC=4,AD=2,则AB的长为( )
 A、1 B、2 C、3 D、46. 在△ABC中,若cosA= ,tanB= ,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形7. 如图,在平行四边形ABCD中,点E是CD边上一点,DE:EC=2:3,连接AE、BE、BD,且AE、BD交于点F.若S△DEF=2,则S△ABE=( )
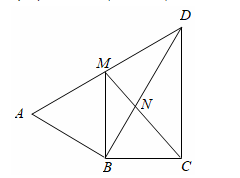
A、1 B、2 C、3 D、46. 在△ABC中,若cosA= ,tanB= ,则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形7. 如图,在平行四边形ABCD中,点E是CD边上一点,DE:EC=2:3,连接AE、BE、BD,且AE、BD交于点F.若S△DEF=2,则S△ABE=( ) A、15.5 B、16.5 C、17.5 D、18.58. 如图,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,连结BE、AD,点M、N分别是线段BE、AD上的两点,且BM= BE,AN= AD,则△CMN的形状是( )
A、15.5 B、16.5 C、17.5 D、18.58. 如图,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,连结BE、AD,点M、N分别是线段BE、AD上的两点,且BM= BE,AN= AD,则△CMN的形状是( )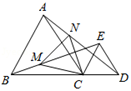 A、等腰三角形 B、直角三角形 C、等边三角形 D、不等边三角形9. 已知1<a<3,则化简 ﹣ 的结果是( )A、2a﹣5 B、5﹣2a C、﹣3 D、310. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
A、等腰三角形 B、直角三角形 C、等边三角形 D、不等边三角形9. 已知1<a<3,则化简 ﹣ 的结果是( )A、2a﹣5 B、5﹣2a C、﹣3 D、310. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )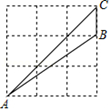 A、 B、 C、 D、11. 如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8m,CD=12m,则点M离地面的高度MH为( )
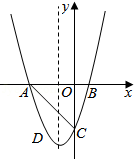
A、 B、 C、 D、11. 如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8m,CD=12m,则点M离地面的高度MH为( ) A、4 m B、 m C、5m D、 m12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b﹣a>c;③4a+2b+c>0;④3a>c;⑤a+b>m(am+b)(m≠1的实数),其中结论正确的有( )
A、4 m B、 m C、5m D、 m12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b﹣a>c;③4a+2b+c>0;④3a>c;⑤a+b>m(am+b)(m≠1的实数),其中结论正确的有( )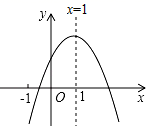 A、①②③ B、②③⑤ C、②③④ D、③④⑤
A、①②③ B、②③⑤ C、②③④ D、③④⑤二、填空题 (每题6分,共18分)
-
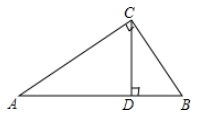
13. 已知关于x的一元二次方程(a﹣2)x2﹣(a2﹣4)x+8=0不含一次项,则a=.14. 某企业两年前创办时的资金为1000万元,现在已有资金1440万元.若设该企业这两年资金的年平均增长率为x,则根据题意可列方程为.15. 若α,β是一元二次方程3x2+2x﹣9=0的两根,则 的值是.16. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB,垂足为D,则tan∠BCD的值是.
 17. 如图,▱ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则▱ABCD的周长等于.
17. 如图,▱ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则▱ABCD的周长等于.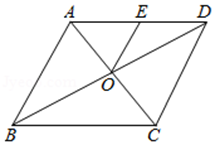 18. 如图,正方形ABCD中,AB=4,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=2,若△ABE与以D、M、N为顶点的三角形相似,则DM=.
18. 如图,正方形ABCD中,AB=4,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=2,若△ABE与以D、M、N为顶点的三角形相似,则DM=.
三、解答题
-
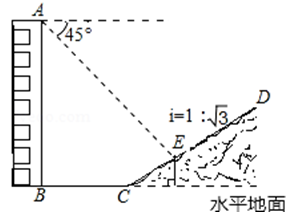
19. 计算:(2﹣ )0+(﹣ )﹣2+2sin45°﹣ .20. 解方程:2x2+x﹣6=0.21. 楼房AB后有一假山,其坡度为i=1: ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.
 22. 某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如图条形统计图和扇形统计图.
22. 某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如图条形统计图和扇形统计图. (1)、本次随机调查的学生人数是人;(2)、请你补全条形统计图;(3)、在扇形统计图中,“A“所在扇形的圆心角等于度;(4)、小明和小华两名同学准备从中各自随机参加一个主题活动,
(1)、本次随机调查的学生人数是人;(2)、请你补全条形统计图;(3)、在扇形统计图中,“A“所在扇形的圆心角等于度;(4)、小明和小华两名同学准备从中各自随机参加一个主题活动,请用画树状图或列表的方式,求他们恰好同时选中“文明礼仪”或“生态环境”主题的概率.
23. 如图,已知在正方形ABCD中,对角线AC与BD交于点O,点M在线段OD上,连结AM并延长交边DC于点E,点N在线段OC上,且ON=OM,连结DN与线段AE交于点H,连结EN、MN.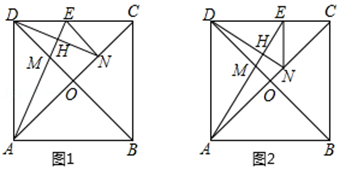 (1)、求证:AM=DN;(2)、如果EN∥BD,求证:四边形DMNE是菱形;(3)、如果EN⊥DC,求证:AN2=NC•AC.24. 某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,针对这种水产品情况,请解答以下问题:(1)、当销售单价定为每千克55元时,计算销售量和月销售利润;(2)、设销售单价为每千克x元,月销售利润为y元,求y与x的关系式;(3)、商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?
(1)、求证:AM=DN;(2)、如果EN∥BD,求证:四边形DMNE是菱形;(3)、如果EN⊥DC,求证:AN2=NC•AC.24. 某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,针对这种水产品情况,请解答以下问题:(1)、当销售单价定为每千克55元时,计算销售量和月销售利润;(2)、设销售单价为每千克x元,月销售利润为y元,求y与x的关系式;(3)、商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?