四川省眉山市东坡区2020-2021学年七年级下学期数学开学试卷

试卷更新日期：2021-04-02 类型：开学考试

进入出卷网下载

一、选择题：本大题共12个小题，每小题4分，共48分.

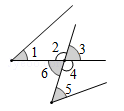
1. ﹣2019的绝对值是（）

A、 $\frac{1}{2019}$ B、﹣2019 C、±2019 D、2019

查看试题解析
2. 下列各式：①1 $\frac{1}{3}$ x；②2•3；③20%x；④a﹣b÷c；⑤ $\frac{m^{2} n^{2}}{3}$ ；⑥x﹣5；其中，不符合代数式书写要求的有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
3. 据报道，2014年我国粮食产量达到540000000000千克，用科学记数法表示这个数为（）

A、 $5.4 \times 10^{10}$ B、 $5.4 \times 10^{11}$ C、 $54 \times 10^{10}$ D、 $0.54 \times 10^{12}$

查看试题解析
4. 如图，下列结论中错误的是（）

A、 $∠ 1$ 与 $∠ 2$ 是同旁内角 B、 $∠ 1$ 与 $∠ 6$ 是内错角 C、 $∠ 2$ 与 $∠ 5$ 是内错角 D、 $∠ 3$ 与 $∠ 5$ 是同位角

查看试题解析
5. 如图，OA⊥OB，若∠1＝55°16′，则∠2的度数是（）

A、35°44′ B、34°84′ C、34°74′ D、34°44′

查看试题解析
6. 下列变形正确的是（）

A、x﹣y+z＝x﹣（y﹣z） B、x﹣y﹣z＝x+（y﹣z） C、x+y﹣z＝x+（y+z） D、x+y+z＝x﹣（﹣y+z）

查看试题解析
7. 若关于x的多项式6x²﹣7x+2mx²+3不含x的二次项，则m＝（）

A、2 B、﹣2 C、3 D、﹣3

查看试题解析
8. 如果代数式x²+2x+7的值等于5，那么代数式-2x²-4x﹣3的值等于（）

A、1 B、﹣1 C、﹣5 D、﹣7

查看试题解析
9. 如图，∠AOB是一直角，∠AOC＝40°，OD平分∠BOC，则∠AOD等于（）

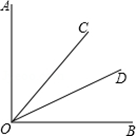A、65° B、50° C、40° D、25°

查看试题解析
10. 如图，直线a∥b，点B在直线b上，AB⊥BC， $∠ 1 = 55 °$ ，则 $∠ 2 =$ （）

A、35° B、45° C、55° D、25°

查看试题解析
11. 下图是一个由多个相同小正方体堆积而成的几何体的俯视图，图中所示数字为该位置小正方体的个数，则这个几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
12. 下列图案是用长度相同的小木棒按一定规律拼搭而成，图案①需8根小木棒，图案②需15根小木棒，…，按此规律，图案⑦需小木棒的根数是（）

A、49 B、50 C、55 D、56

查看试题解析

二、填空题（本大题共6个小题，每题4分，满分24分）

13. 如果温度上升3℃记作+3℃，那么下降5℃记作.

查看试题解析
14. 若单项式xy^m与2xⁿ^﹣¹y³是同类项，则m+n＝.

查看试题解析
15. 一个角的补角是这个角余角的3倍，则这个角是度．

查看试题解析
16. 如图，OP∥QR∥ST，若∠2＝100°，∠3＝120°，则∠1＝.

查看试题解析
17. 已知线段 $A B = 16 c m$ ，直线 $A B$ 上有一点C，并且 $B C = 6 c m$ ，点D是线段 $A C$ 的中点，则线段 $D B =$ ．

查看试题解析
18. 【阅读】计算1+3+3²+3³+……+3¹⁰⁰的值.
令S＝1+3+3²+3³+……+3¹⁰⁰ ，则3S＝3+3²+3³+……+3¹⁰¹ ，因此3S﹣S＝3¹⁰¹﹣1，

所以S＝ $\frac{3^{101} - 1}{2}$ ，即S＝1+3+3²+3³+……+3¹⁰⁰＝ $\frac{3^{101} - 1}{2}$ .

依照以上推理，计算：1﹣5+5²﹣5³+5⁴﹣5⁵+……+5²⁰¹⁸﹣5²⁰¹⁹+ $\frac{5^{2020}}{6}$ ＝.

查看试题解析

三、解答题：19-20 每小题8分，21-25 每小题10分，26 题12分，共78分.

19. 计算： $5 \times (- 2) + (- 8) \div (- 2)$

查看试题解析
20. 计算： $- 1^{2} - (- 10) \div \frac{1}{2} \times 2 + {(- 4)}^{2}$

查看试题解析
21. 先化简，再求值.3a²b﹣[2ab²﹣2（a²b﹣2ab²）]，其中a、b满足等式（2a﹣1）²+|b+2|＝0.

查看试题解析
22. 已知：如图，点B和点D在线段AC上，若BD＝ $\frac{1}{4}$ AB＝ $\frac{1}{3}$ CD，E为线段AB的中点，BC＝6cm，求线段ED的长度.

查看试题解析
23. 有理数a，b，c在数轴上的位置如图所示，且|a|＝|b|，化简|c﹣a|+|c﹣b|+|a+b|.

查看试题解析
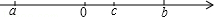24. 已知：如图，DG⊥BC，AC⊥BC，EF⊥AB，∠1＝∠2，求证：CD⊥AB.

证明：∵DG⊥BC，AC⊥BC（已知）

∴∠DGC＝∠ACB＝90°（   ）

∴∠DGC+∠ACB＝180°

∴▲∥▲（   ）

∴∠2＝▲（   ）

∵∠1＝∠2（已知）

∴∠1＝▲（   ）

∴EF∥CD （   ）

∴∠AEF＝▲（   ）

∵EF⊥AB （   ）

∴∠AEF＝90°

∴∠ADC＝90°

∴CD⊥AB.

查看试题解析
25. 某校为适应新的中考要求，决定为体育组添置一批体育器材.学校准备在网上订购一批某品牌足球和跳绳，在查阅天猫网店后发现足球每个定价140元，跳绳每条定价30元.现有A、B两家网店均提供包邮服务，并提出了各自的优惠方案.A网店：买一个足球送一条跳绳；B网店：足球和跳绳都按定价的90%付款.已知要购买足球60个，跳绳x条（x＞60）

(1)、若在A网店购买，需付款元（用含x的代数式表示）；若在B网店购买，需付款元（用含x的代数式表示）；

(2)、若x＝100时，通过计算说明此时在哪家网店购买较为合算？

(3)、当x＝100时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法，并计算需付款多少元？

查看试题解析
26. 如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F.

(1)、当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为.

(2)、当△PMN所放位置如图②所示时，PN交CD于点H.请猜想∠PFD与∠AEM的数量关系并证明.

(3)、在（2）的条件下，若MN与CD交于点O，且∠DON＝20°，∠PEB＝15°，求∠N的度数.

查看试题解析