浙江省湖州市五中2021届数学中考一模试卷

试卷更新日期：2021-04-02 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，共30分）

1. ﹣2021的相反数是（）

A、﹣ $\frac{1}{2021}$ B、 $\frac{1}{2021}$ C、2021 D、﹣2021

查看试题解析
2. 在下列运算中，计算正确的是（）

A、a³•a²=a⁶ B、a⁸÷a²=a⁴ C、（a²）³=a⁶ D、a²+a²=a⁴

查看试题解析
3. 如图，桌面上有一个球和一个圆柱形茶叶罐靠在一起，则主视图正确的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，已知A，B，C在⊙O上， $\overset{⌢}{A C B}$ 为优弧，下列选项中与∠AOB相等的是（）

A、∠B+∠C B、4∠B C、4∠A D、2∠C

查看试题解析

5. 某一段时间，小芳测得连续五天的日最低气温后，整理得出表（有两个数据被遮盖），被遮盖的两个数据依次是（）

日期	一	二	三	四	五	方差	平均气温
最低气温	1℃	﹣1℃	2℃	0℃	■	■	1℃

A、3℃，2 B、3℃，

\frac{6}{5}

C、2℃，2 D、2℃，

\frac{8}{5}

查看试题解析

6. 如图，某小区规划在一个长AD＝40m，宽AB＝26m的矩形场地ABCD上修建三条同样宽的通道（图中阴影部分），使其中两条与AB平行，另一条与AD平行，其余部分种植花草，要使每一块种植花草的场地面积都是144m².若设通道的宽度为x（m），则根据题意所列的方程是（）

A、（40﹣x）（26﹣2x）＝144×6 B、（40﹣2x）（26﹣x）＝144×6 C、（40﹣2x）（26﹣x）＝144÷6 D、（40﹣x）（26﹣2x）＝144÷6

查看试题解析
7. 已知a＜0＜b，那么下列不等式组中一定有解的是（）

A、 ${\begin{matrix} x > - a \\ x < - b \end{matrix}$ B、 ${\begin{matrix} x > - b \\ x < - a \end{matrix}$ C、 ${\begin{matrix} x > a \\ x < - b \end{matrix}$ D、 ${\begin{matrix} x > - a \\ x < b \end{matrix}$

查看试题解析
8. 如图是一个3×2的长方形网格，组成网格的小长方形长为宽的2倍，△ABC的顶点都是网格中的格点，则sin∠BAC的值（）

A、 $\frac{\sqrt{13}}{13}$ B、 $\frac{5 \sqrt{13}}{78}$ C、 $\frac{6 \sqrt{13}}{65}$ D、 $\frac{5 \sqrt{13}}{26}$

查看试题解析
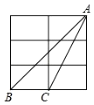9. 如图，在平面直角坐标系中，⊙O的直径2 $\sqrt{3}$ ，直线AB的函数解析式为y＝ $\frac{\sqrt{3}}{3}$ x﹣1，交坐标轴于点A和点B，将线段AB作平移变换，使所得的线段的两端都落在⊙O上，则平移后A点所对应的点的坐标是（）

A、（ $\frac{\sqrt{3} - \sqrt{2}}{2}$ ， $\frac{1 + \sqrt{6}}{2}$ ）或（ $\frac{\sqrt{3} + \sqrt{2}}{2}$ ， $\frac{1 - \sqrt{6}}{2}$ ） B、（ $\frac{\sqrt{3} - \sqrt{2}}{2}$ ， $\frac{1 + \sqrt{6}}{2}$ ）或（ $\frac{\sqrt{3} + \sqrt{2}}{2}$ ， $\frac{1 + \sqrt{6}}{2}$ ） C、（ $\frac{\sqrt{3} - \sqrt{2}}{2}$ ， $\frac{\sqrt{6} - 1}{2}$ ）或（ $\frac{\sqrt{3} + \sqrt{2}}{2}$ ， $\frac{1 + \sqrt{6}}{2}$ ） D、（ $\frac{\sqrt{3} - \sqrt{2}}{2}$ ， $\frac{1 + \sqrt{6}}{2}$ ）或（ $\frac{- \sqrt{3} + \sqrt{2}}{2}$ ， $\frac{1 - \sqrt{6}}{2}$ ）

查看试题解析
10. 如图，在反比例函数y＝ $\frac{m}{x}$ （m为常数，且m＞0）第一象限内图象上取一点P，连接OP₁ ，过P₁作P₁A₁⊥x轴，垂足为A₁；在OA₁的延长线上截取A₁B₁＝OA₁ ，过B₁作OP₁的平行线交反比例函数的图象于P₂ ，过P₂作P₂A₂⊥x轴，垂足为A₂；在OA₂的延长线上截取A₂B₂＝B₁A₂.连接P₁B₁ ， P₂B₂ ，则 $\frac{O A_{1}}{O A_{2}}$ 的值是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{2}$ m C、（ $\sqrt{2}$ ﹣1）m D、 $\sqrt{2}$ ﹣1

查看试题解析

二、填空愿（本大题共6小题，共24分）

11. 分解因式：x²﹣y²= ．

查看试题解析
12. 一只盒子中有红球m个，白球8个，黑球n个，每个球除颜色外都相同，从中任取一个球，如果取得红球或黑球的概率与取得白球的概率相同，那么m与n的关系是.

查看试题解析
13. 如图，已知圆锥的底面半径为3，母线长为4，则它的侧面积是.

查看试题解析
14. 如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连接BD并延长交EG于点T，交FG于点P，则GT＝.

查看试题解析
15. 当﹣7≤x≤a时，二次函数y＝﹣ $\frac{1}{2}$ （x+3）²+5恰好有最大值3，则a＝.

查看试题解析
16. 如图，矩形OABC中，点A，点C分别在x轴，y轴上，D为边BC上的一动点，现把△OCD沿OD对折，C点落在点P处.已知点B的坐标为（2 $\sqrt{3}$ ，2）.

(1)、在点D沿BC从点C运动至点B的过程中，设点P经过的路径长度为1，则l的值；

(2)、在点D沿BC从点C运动至点B的过程中，若点P落在同一条直线y＝kx+4上的次数为2次，请直接写出k的取值范围.

查看试题解析

三、解答题（本大题8小题，共66分）

17. 计算： $3 - 2 \sqrt{5} + 2$ .

查看试题解析
18. 先化简，再求值 $(\frac{1}{x} - \frac{2}{x - 1}) \div \frac{1}{x^{2} - x}$ ，其中x为整数且满足不等式组 ${\begin{matrix} x + 1 < 3 \\ 2 x + 9 < 5 \end{matrix}$ .

查看试题解析
19. 如图，已知BE⊥AD，CF⊥AD，且BE＝CF.

(1)、请你判断AD是△ABC的中线还是角平分线？说明你判断的理由.

(2)、连接BF，CE，求证：四边形BECF是平行四边形.

查看试题解析
20. 为了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等5项体育活动的喜欢程度，某校随机抽查部分学生，对他们最喜欢的体育项目（每人只选一项）进行了问卷调查，并将统计数据绘制成如下两幅不完整的统计图：
请解答下列问题：

(1)、m＝%，这次共抽取了名学生进行调查；请补全条形统计图；

(2)、若全校有800名学生，则该校约有多少名学生喜爱打篮球？

(3)、学校准备从喜欢跳绳活动的4人（二男二女）中随机选取2人进行体能测试，求抽到一男一女学生的概率是多少？

查看试题解析
21. 如图，在等腰直角三角形ABC中，∠ABC＝90°，AB＝BC＝4，⊙B与AB、BC交于E、F，点P是弧EF上的一个动点，连接PC，线段PC绕P点逆时针旋转90°到PD，连接CD，AD.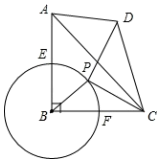

(1)、求证：△BPC∽△ADC；

(2)、当四边形ABCD满足AD∥CB且是面积为12时，求⊙B的半径.

查看试题解析

22. 某手机专卖店销售A，B两种型号的手机，如表是近两周的销售情况：

销售时段	销售数量		销售利润
销售时段	A型	B型	销售利润
第一周	3台	5台	1800元
第二周	4台	10台	3000元

(1)、求每台A型手机和B型手机的销售利润；

(2)、该手机专卖店计划一次购进两种型号的手机共100台，其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台，这100台手机的销售总利润为y元.

①求y关于x的函数表达式；

②该商店购进A型号和B型号手机各多少台，才能使销售总利润最大？

(3)、实际进货时，厂家对A型号手机的出厂价提高a（0＜a＜100）元，对B型号手机的出厂价下降a（0＜a＜100）元，且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变，请根据以上信息及（2）中条件，设计出使这100台手机销售总利润最大的进货方案.

查看试题解析

23. 如图，已知抛物线y＝x²+bx+c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C（0，﹣3），对称轴是直线x＝1，直线BC与抛物线的对称轴交于点D.

(1)、求抛物线的函数表达式；

(2)、点E为y轴上一动点.
①若CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限，当线段PQ＝ $\frac{3}{4}$ AB时，求∠CED的正切值；

②若点G是直线x＝1上一点，当△CEG与△AOC相似时，请直接写出点E的坐标.

查看试题解析
24. AB为⊙O的直径，弦CD⊥AB，垂足为H，F为弧BC上一点，且∠FBC＝∠ABC，连接DF，分别交BC、AB于E、G.

(1)、如图1，求证：DF⊥BC；

(2)、如图2，连接EH，过点E作EM⊥EH，EM交⊙O于点M，交AB于点N.
①求证：EN＝GN；

②连接OC，求证：△CHO≌△HEN.

查看试题解析