四川省泸州市龙马潭区2021届九年级下学期数学第一次诊断性考试试卷

试卷更新日期：2021-04-02 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列四个数中，最大的有理数是（）

A、-1 B、-2019 C、 $\sqrt{3}$ D、0

查看试题解析
2. 下列符号中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 习近平总书记提出了未来五年“精准扶贫”的战略构想，意味着每年要减贫约11700000人，将数据11700000用科学记数法表示为（）

A、1.17×10⁷ B、11.7×10⁶ C、0.117×10⁷ D、1.17×10⁸

查看试题解析
4. 下列运算正确的是（）

A、 $x^{3} \cdot x^{2} = x^{6}$ B、 $3 a^{3} + 2 a^{2} = 5 a^{5}$ C、 ${(m^{2} n)}^{3} = m^{6} n^{3}$ D、 $x^{8} \div x^{4} = x^{2}$

查看试题解析
5. 函数y＝ $\frac{\sqrt{x - 2}}{x - 1}$ 中自变量x的取值范围是（）

A、x≥2且x≠1 B、x≥2 C、x≠1 D、﹣2≤x＜1

查看试题解析
6. 下列图是由5个大小相同的小立方体搭成的几何体，主视图和左视图相同的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，AB//CD，点E在CA的延长线上若∠BAE =50°，则∠ACD的大小为（）

A、120 $°$ B、130 $°$ C、140 $°$ D、150 $°$

查看试题解析
8. 在学校的体育训练中，小杰投掷实心球的7次成绩如统计图所示，则这7次成绩的中位数和平均数分别是 $($ 　　 $)$

A、 $9.7 m$ ， $9.9 m$ B、 $9.7 m$ ， $9.8 m$ C、 $9.8 m$ ， $9.7 m$ D、 $9.8 m$ ， $9.9 m$

查看试题解析
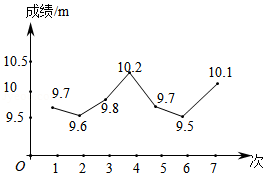9. 如图，四边形ABCD内接于⊙O，F是 $\overset{⌢}{C D}$ 上一点，且 $\overset{⌢}{D F} = \overset{⌢}{B C}$ ，连接CF并延长交AD的延长线于点E，连接AC，若∠ABC=105°，∠BAC=25°，则∠E的度数为（　　）

A、45° B、50° C、55° D、60°

查看试题解析
10. 关于x的方程 $\frac{k}{2 x - 4} - 1 = \frac{x}{x - 2}$ 的解为正数，则k的取值范围是（）

A、 $k > - 4$ B、 $k < 4$ C、 $k > - 4$ 且 $k \neq 4$ D、 $k < 4$ 且 $k \neq - 4$

查看试题解析
11. 如图，正方形 $A B C D$ 中，点 $E$ 、 $F$ 分别在边 $C D$ ， $A D$ 上， $B E$ 与 $C F$ 交于点 $G$ .若 $B C = 4$ ， $D E = A F = 1$ ，则 $G F$ 的长为（）

A、 $\frac{13}{5}$ B、 $\frac{12}{5}$ C、 $\frac{19}{5}$ D、 $\frac{16}{5}$

查看试题解析
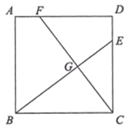12. 已知二次函数y=x²﹣2mx（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m的值是（）

A、 $\frac{3}{2}$ B、 $\sqrt{2}$ C、 $\frac{3}{2}$ 或 $\sqrt{2}$ D、 $- \frac{3}{2}$ 或 $\sqrt{2}$

查看试题解析

二、填空题

13. 分解因式： $x^{2} y - 4y =$ ．

查看试题解析
14. 如图，已知圆锥的高为 $\sqrt{3}$ ，高所在直线与母线的夹角为30°，圆锥的侧面积为.

查看试题解析
15. 设 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} + 3 x - 3 = 0$ 的两个实数根，则 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}}$ 的值为.

查看试题解析
16. 如图，直线 $y = - \frac{3}{4} x + 3$ 与x轴、y轴分别交于点A、B；点Q是以C（0，﹣1）为圆心、1为半径的圆上一动点，过Q点的切线交线段AB于点P，则线段PQ的最小是．

查看试题解析

三、解答题

17. 计算： ${(1 - \sqrt{3})}^{0} + | - \sqrt{2} | - 2 cos 45 ° + {(\frac{1}{4})}^{- 1}$

查看试题解析
18. 先化简，再求值： $(m + 2 + \frac{1}{m}) • \frac{m}{m + 1}$ ，其中 $m = - 4 + \sqrt{3}$

查看试题解析
19. 如图，AB//CD，AB=CD点E、F在BC上，且BF=CE.

(1)、求证：△ABE≌△DCF

(2)、求证：AE//DF.

查看试题解析
20. 抚顺某中学为了解八年级学生的体能状况，从八年级学生中随机抽取部分学生进行体能测试，测试结果分为A，B，C，D四个等级．请根据两幅统计图中的信息回答下列问题：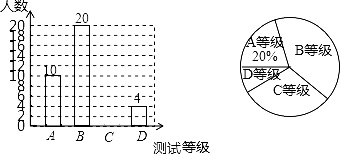

(1)、本次抽样调查共抽取了多少名学生？

(2)、求测试结果为C等级的学生数，并补全条形图；

(3)、若该中学八年级共有700名学生，请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名？

(4)、若从体能为A等级的2名男生2名女生中随机的抽取2名学生，做为该校培养运动员的重点对象，请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率．

查看试题解析
21. 某文具店最近有A，B两款毕业纪念册比较畅销，近两周的销售情况是：第一周A款销售数量是15本，B款销售数量是10本，销售总价是230元；第二周A款销售数量是20本，B款销售数量是10本，销售总价是280元.

(1)、求A，B两款毕业纪念册的销售单价；

(2)、若某班准备用不超过529元购买这两种款式的毕业纪念册共60本，求最多能够买多少本A款毕业纪念册.

查看试题解析
22.
盐城电视塔是我市标志性建筑之一．如图，在一次数学课外实践活动中，老师要求测电视塔的高度AB．小明在D处用高1.5m的测角仪CD，测得电视塔顶端A的仰角为30°，然后向电视塔前进224m到达E处，又测得电视塔顶端A的仰角为60°．求电视塔的高度AB．（ $\sqrt{3}$ 取1.73，结果精确到0.1m）

查看试题解析
23. 如图，一次函数 $y = k x + b (k \neq 0)$ 的图象与反比例函数 $y = \frac{m^{2} - 3 m}{x}$ （ $m \neq 0$ 且 $m \neq 3$ ）的图象在第一象限交于点 $A$ 、 $B$ ，且该一次函数的图象与 $y$ 轴正半轴交于点 $C$ ，过 $A$ 、 $B$ 分别作 $y$ 轴的垂线，垂足分别为 $E$ 、 $D$ .已知 $A (4 ， 1)$ ， $C E = 4 C D$ .

(1)、求 $m$ 的值和反比例函数的解析式；

(2)、若点 $M$ 为一次函数图象上的动点，求 $O M$ 长度的最小值.

查看试题解析
24. 如图，△ABC内接于⊙O，且AB为⊙O的直径.∠ACB 的平分线交⊙O于点D，过点D作直线l交CA的延长线于点P，且∠ADP=∠BCD，过点A作AE丄CD于点E，过点B作BF丄CD于点F.

(1)、求证：DP//AB；

(2)、求证：PD是⊙O的切线；

(3)、若AC=6，BC=8，求线段PD的长.

查看试题解析
25. 如图，已知抛物线y= $\frac{1}{3}$ x²+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（-9，10），AC∥x轴，点P是直线AC下方抛物线上的动点.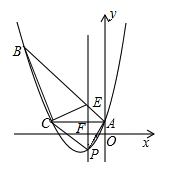

(1)、求抛物线的解析式；

(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；

(3)、当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由.

查看试题解析