湖南省长沙市青竹湖2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-04-02 类型:期末考试
一、单选题
-
1. 下列哪些图形是通过平移可以得到的( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各数是无理数的是( )A、 B、 C、 D、-63. 2019年“国庆”期间,我市接待海内外游客共690000人次,将690000这个数用科学记数法表示为( )A、 B、 C、 D、4. 多项式 的次数与项数分别是( )A、2,4 B、3,3 C、3,4 D、4,35. 如图,能判定 的条件是( )
2. 下列各数是无理数的是( )A、 B、 C、 D、-63. 2019年“国庆”期间,我市接待海内外游客共690000人次,将690000这个数用科学记数法表示为( )A、 B、 C、 D、4. 多项式 的次数与项数分别是( )A、2,4 B、3,3 C、3,4 D、4,35. 如图,能判定 的条件是( ) A、 B、 C、 D、6. 若代数式 和 互为相反数,则x的值为( )A、 B、 C、 D、7. 如图,已知射线OA⊥射线OB, 射线OA表示北偏西25°的方向,则射线OB表示的方向为( )
A、 B、 C、 D、6. 若代数式 和 互为相反数,则x的值为( )A、 B、 C、 D、7. 如图,已知射线OA⊥射线OB, 射线OA表示北偏西25°的方向,则射线OB表示的方向为( )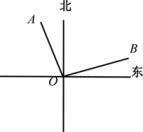 A、北偏东65° B、北偏东55° C、北偏东75° D、东偏北75°8. 下列命题中是假命题的是( )A、两直线平行,同旁内角互补 B、同位角相等,两直线平行 C、若a∥b,a⊥c,那么b⊥c D、相等的角是对顶角9. 如图,将直尺与三角尺叠放在一起,如果 ,那么 的度数为( )
A、北偏东65° B、北偏东55° C、北偏东75° D、东偏北75°8. 下列命题中是假命题的是( )A、两直线平行,同旁内角互补 B、同位角相等,两直线平行 C、若a∥b,a⊥c,那么b⊥c D、相等的角是对顶角9. 如图,将直尺与三角尺叠放在一起,如果 ,那么 的度数为( )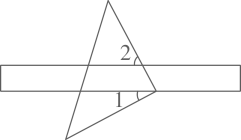 A、62° B、56° C、28° D、72°10. 如图,已知 .则结论① ;② 平分 ;③ ;④ .正确的是( )
A、62° B、56° C、28° D、72°10. 如图,已知 .则结论① ;② 平分 ;③ ;④ .正确的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 已知 ,则 的余角为.12. 关于 的方程 的解是 ,则 的值为 .13. 如图,将 沿着射线 的方向平移,得到 ,若 ,则平移的距离为.
 14. 若 ,且 , 是两个连续的整数,则a+b的值是.15. 若 ,则 .16. 如图,将长方形纸片ABCD折叠,使顶点A , C重合,折痕为EF.若∠BAE=28° , 则∠AEF的大小为°.
14. 若 ,且 , 是两个连续的整数,则a+b的值是.15. 若 ,则 .16. 如图,将长方形纸片ABCD折叠,使顶点A , C重合,折痕为EF.若∠BAE=28° , 则∠AEF的大小为°.
三、解答题
-
17. 计算: .18. 先化简,再求值:
,其中 , .
19. 已知: 的立方根是 , 的算术平方根3, 是 的整数部分.(1)、求 的值;(2)、求 的平方根.20. 如图已知点C为AB上一点,AC=18cm,CB= AC,D、E分别为AC、AB的中点,求DE的长. 21. 列一元一次方程解应用题:
21. 列一元一次方程解应用题:某水果店计划购进 . 两种水果,下表是 . 这两种水果的进货价格:
水果品种
进货价格(元 )
10
15
(1)、若该水果店要花费600元同时购进两种水果共 ,则购进 . 两种水果各为多少 ?(2)、若水果店将 种水果的售价定为 元 ,要使购进的这批水果在完全售出后达到 的利润率, 种水果的售价应该定为多少?22. 如图,点A,O,E在同一条直线上,∠AOB=40°,∠COD=28°,OD平分∠COE,求∠DOB的度数.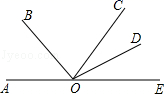 23. 如图,在三角形ABC中,D,E,F分别是三边上的点,且DE平分∠ADF,∠ADF=2∠DFB.
23. 如图,在三角形ABC中,D,E,F分别是三边上的点,且DE平分∠ADF,∠ADF=2∠DFB.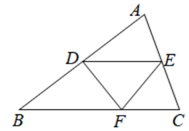 (1)、判断DE与BC是否平行,并说明理由.(2)、若EF∥AB,∠DFE=3∠CFE,求∠ADE的度数.24. 已知多项式 是关于 的二次多项式,且二次项系数为 ,数轴上两点 对应的数分别为 .
(1)、判断DE与BC是否平行,并说明理由.(2)、若EF∥AB,∠DFE=3∠CFE,求∠ADE的度数.24. 已知多项式 是关于 的二次多项式,且二次项系数为 ,数轴上两点 对应的数分别为 . (1)、 , , 线段 ;(2)、若数轴上有一点 ,使得 ,点 为 的中点,求 的长;(3)、有一动点 从点 出发,以1个单位每秒的速度向终点 运动,同时动点 从点 出发,以 个单位每秒的速度在数轴上作同向运动,设运动时间为 秒( ),点 为线段 的中点,点 为线段 的中点,点 在线段 上且 ,在 的运动过程中,求 的值.25. 已知,如图1,射线 分别与直线 相交于 两点, 的平分线与直线 相交于点 ,射线 交 于点 ,设 , ,且 .
(1)、 , , 线段 ;(2)、若数轴上有一点 ,使得 ,点 为 的中点,求 的长;(3)、有一动点 从点 出发,以1个单位每秒的速度向终点 运动,同时动点 从点 出发,以 个单位每秒的速度在数轴上作同向运动,设运动时间为 秒( ),点 为线段 的中点,点 为线段 的中点,点 在线段 上且 ,在 的运动过程中,求 的值.25. 已知,如图1,射线 分别与直线 相交于 两点, 的平分线与直线 相交于点 ,射线 交 于点 ,设 , ,且 . (1)、 °, °;直线 与 的位置关系是;(2)、如图2,若点 是射线 上任意一点,且 ,试找出 与 之间存在的数量关系,证明你的结论;(3)、若将图中的射线 绕着端点 逆时针方向旋转(如图3),分别与 相交于点 和 时,作 的角平分线 与射线 相交于点 ,问在旋转的过程中 的值变不变?若不变,请求出其值;若变化,请说明理由.
(1)、 °, °;直线 与 的位置关系是;(2)、如图2,若点 是射线 上任意一点,且 ,试找出 与 之间存在的数量关系,证明你的结论;(3)、若将图中的射线 绕着端点 逆时针方向旋转(如图3),分别与 相交于点 和 时,作 的角平分线 与射线 相交于点 ,问在旋转的过程中 的值变不变?若不变,请求出其值;若变化,请说明理由.