河南省郑州市登封市2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 如果股票指数上涨5点记作+5，那么股票指数下跌10点记作（）

A、+10 B、-10 C、-5 D、-15

查看试题解析
2. 如图是由一些大小相同的小正方体堆成的几何体，则从正面看该几何体所得到的图形是（）

A、 B、 C、 D、

查看试题解析
3. 世界卫生组织11月22日公布的数据显示，全球累计新冠确诊病例达57882183例，这个数据用科学记数法表示为（）

A、 $5.7882183 \times 10^{6}$ B、 $57.882183 \times 10^{7}$ C、 $5.7882183 \times 10^{7}$ D、 $0.57882183 \times 10^{7}$

查看试题解析
4. 若关于 $x$ 的方程 $2 x - a = 3$ 的解为 $x = 1$ ，则 $a$ 的值等于（）

A、5 B、-5 C、1 D、-1

查看试题解析
5. 已知有理数 $a$ ， $b$ 在数轴上的位置如图所示，则下列结论中正确的是（）

A、 $a < b$ B、 $| a | < | b |$ C、 $\frac{a}{b} > 0$ D、 $a + b > 0$

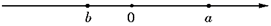查看试题解析
6. 将标有“全面依法治国”的小正方体展开后如图所示，则原正方体中和“国”字相对的面上的字是（）

A、法 B、依 C、全 D、面

查看试题解析
7. 将一个圆分割成三个扇形，它们的面积之比为 $3 : 4 : 5$ ，则最小扇形的圆心角的度数为（）

A、 $120 °$ B、 $90 °$ C、 $270 °$ D、 $180 °$

查看试题解析
8. 下列说法正确的有（）
①一个数的相反数不是正数就是负数；②海拔 $- 300 m$ 表示比海平面低 $300 m$ ；③负分数不是有理数；④由两条射线组成的图形叫做角；⑤把一个角放到一个放大5倍的放大镜下观看，角的度数也扩大5倍.

A、0个 B、1个 C、2个 D、3个

查看试题解析
9. 按如图所示的运算程序，能使输出结果为10的是（）

A、 $x = 4$ ， $y = - 2$ B、 $x = 2$ ， $y = - 4$ C、 $x = - 2$ ， $y = 4$ D、 $x = - 2$ ， $y = - 2$

查看试题解析
10. 如图，一个动点从原点 $O$ 开始向左运动，每秒运动1个单位长度，并且规定：每向左运动3秒就向右运动2秒，则该动点运动到第2021秒时所对应的数是（）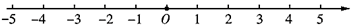

A、-406 B、-405 C、-2020 D、-2021

查看试题解析

二、填空题

11. 单项式 $- \frac{4}{3} π a b^{3} c$ 的次数是.

查看试题解析
12. 张老师调整教室桌椅时，为了将一列课桌对齐，将这列课桌的最前边一张和最后边一张拉一条线，其余课桌按线摆放，这样做用到的数学知识是.

查看试题解析
13. 9时20分时，时钟上的时针和分针的夹角是.

查看试题解析
14. 若 $- 4 x^{a + 5} y^{3} + x^{3} y^{2 - b} = - 3 x^{3} y^{3}$ ，则 $a b$ 的值.

查看试题解析
15. 线段 $A B = 15$ ，点 $P$ 从点 $A$ 开始向点 $B$ 以每秒1个单位长度的速度运动，点 $Q$ 从点 $B$ 开始向点 $A$ 以每秒2个单位长度的速度运动，当其中一个点到达终点时另一个点也随之停止运动，当 $A P = 2 P Q$ 时， $t$ 的值为.

查看试题解析

三、解答题

16. 计算：

(1)、 $- 3 - 24 \times (\frac{1}{4} - \frac{1}{6})$ ；

(2)、 $- {(- 2)}^{3} - {(- \frac{1}{2})}^{2} \times (- 4) + {(- 1)}^{2021}$ .

查看试题解析
17. 解方程：

(1)、 $3 (x - 4) - 5 (x - 2) = 2$ ；

(2)、 $\frac{0.2 x + 1}{0.5} = \frac{0.1 x - 0.1}{0.2} + 1$ .

查看试题解析
18. 求代数式的值： $- 2 (x^{2} y + x y^{2}) - 2 (x^{2} y - 1) - 2 x y^{2} - 2$ ，其中 $x = - 2$ ， $y = 2$ .

查看试题解析
19. 已知线段 $A B$ ，请用尺规按下列要求作图，保留作图痕迹，不写作法：

(1)、延长线段 $B A$ 到 $C$ ，使 $A C = 3 A B$ ；

(2)、延长线段 $A B$ 到 $D$ ，使 $A D = 3 A B$ ；

(3)、在上述作图条件下，若 $C B = 8 cm$ ，求 $B D$ 的长度.

查看试题解析
20. 如图，已知 $∠ A O F = ∠ B O C = 110 °$ ， $∠ B O F = 80 °$ ， $O E$ 是 $∠ A O C$ 的平分线，求 $∠ C O E$ 的度数.

查看试题解析
21. 整体思想就是在解决数学问题时把某些式子或图形看成一个整体，把握它们之间的关联，进行有目的、有意识的整体处理.请利用你对整体思想的理解解决下列问题.

(1)、若 $2 x + 3 y = 5$ ，则代数式 $4 x + 6 y + 3 =$ ；（直接填入答案）

(2)、若 $a + b = 8$ ， $a b = - 4$ ，求代数式 $(4 a - 3 b - 2 a b) - (a - 6 b - a b)$ 的值；

(3)、若 $a^{2} + a b = 3$ ， $2 b^{2} + 3 a b = 8$ ，求代数式 $a^{2} + 10 a b + 6 b^{2}$ 的值.

查看试题解析
22. 小明研究规律方程的时候遇到了下面一组方程：
① $\frac{x}{4} + \frac{x - 1}{2} = 1$ ；

② $\frac{x}{6} + \frac{x - 2}{2} = 1$ ；

③ $\frac{x}{8} + \frac{x - 3}{2} = 1$ ；

④…

(1)、请聪明的你帮小明写出一条这组规律方程的信息；

(2)、小明通过计算发现，第一个方程的解是 $x = 2$ ，第二个方程的解为 $x = 3$ ，因此他就大胆地推测出第三个方程的解为 $x = 4$ ，并写出了第四个方程.请你验证一下小明的推测是否正确，如果正确，请你写出验证过程，并写出第四个方程；如果不正确，请说明理由；

(3)、你能根据以上解决问题的经验直接写出符合上述规律，解为 $x = n$ （ $n$ 为正整数，且 $n \geq 2$ ）的方程吗？

查看试题解析
23. 用若干个大小相同的小立方块搭建一个几何体，从正面和上面观察这个几何体得到下面两幅形状图.

（从正面看）（从上面看）

(1)、请画出一种从左面看这个几何体得到的形状图；

(2)、搭建这个几何体最少要用 $a =$ 个小立方块，最多用 $b =$ 个小立方块；

(3)、在（2）的条件下，若有理数 $x$ ， $y$ 满足 $| x | = a$ ， $| y | = b$ ，且 $x + y < 0$ ，求 $x y$ 的值.

查看试题解析