重庆市渝北区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-02 类型:期末考试
一、单选题
-
1. 实数5的相反数是( )A、 B、5 C、 D、2. 下面是同学们利用图形变化的知识设计的一些美丽的图案,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 计算 ,结果是( )A、 B、 C、 D、4. 如图,⊙O是△ABC的外接圆,∠A= ,则∠BOC的大小为( )
3. 计算 ,结果是( )A、 B、 C、 D、4. 如图,⊙O是△ABC的外接圆,∠A= ,则∠BOC的大小为( )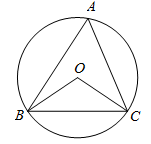 A、40° B、30° C、80° D、100°5. 估计 的值应在( )A、4和5之间 B、3和4之间 C、2和3之间 D、1和2之间6. 下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,⋯,按此规律排列下去,第⑥个图形中实心圆点的个数为( )
A、40° B、30° C、80° D、100°5. 估计 的值应在( )A、4和5之间 B、3和4之间 C、2和3之间 D、1和2之间6. 下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,⋯,按此规律排列下去,第⑥个图形中实心圆点的个数为( ) A、18 B、19 C、20 D、217. 下列命题中,假命题是( )A、如果直角三角形中有一个角为 ,那么它所对的直角边等于斜边的一半 B、如果三角形中有两个角的和等于第三个角,那么这个三角形是直角三角形 C、如果三角形中有两条边的和等于第三条边的平方,那么这个三角形是直角三角形 D、如果三角形中一边上的中线等于这条边的一半,那么这个三角形是直角三角形8. 以下尺规作图中,点 为线段 边上一点,一定能得到线段 的是( )A、
A、18 B、19 C、20 D、217. 下列命题中,假命题是( )A、如果直角三角形中有一个角为 ,那么它所对的直角边等于斜边的一半 B、如果三角形中有两个角的和等于第三个角,那么这个三角形是直角三角形 C、如果三角形中有两条边的和等于第三条边的平方,那么这个三角形是直角三角形 D、如果三角形中一边上的中线等于这条边的一半,那么这个三角形是直角三角形8. 以下尺规作图中,点 为线段 边上一点,一定能得到线段 的是( )A、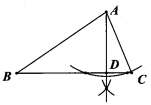 B、
B、 C、
C、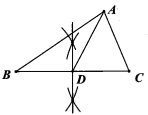 D、
D、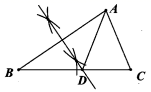 9. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托,折回索子却量竿,却比竿子短一托”,其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长 尺;如果将绳索对半折后再去量竿,就比竿短 尺.若设竿长 尺,绳索长 尺,则符合题意的方程组为( )A、 B、 C、 D、10. 如图,在等边三角形 中,点 , 分别是边 , 上的点.将 沿 翻折,点 正好落在线段 上的点 处,使得 .若 ,则 的长度为( )
9. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托,折回索子却量竿,却比竿子短一托”,其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长 尺;如果将绳索对半折后再去量竿,就比竿短 尺.若设竿长 尺,绳索长 尺,则符合题意的方程组为( )A、 B、 C、 D、10. 如图,在等边三角形 中,点 , 分别是边 , 上的点.将 沿 翻折,点 正好落在线段 上的点 处,使得 .若 ,则 的长度为( ) A、 B、 C、 D、11. 若整数 使得关于 的方程 的解为非负数,且使得关于 的一元一次不等式组 至少有3个整数解,则所有符合条件的整数 的和为( )A、23 B、25 C、27 D、2812. 如图,在平面直角坐标系中, 轴于点 , ,双曲线 过点 ,交 于点 ,连接 , .若 , ,则 的值为( )
A、 B、 C、 D、11. 若整数 使得关于 的方程 的解为非负数,且使得关于 的一元一次不等式组 至少有3个整数解,则所有符合条件的整数 的和为( )A、23 B、25 C、27 D、2812. 如图,在平面直角坐标系中, 轴于点 , ,双曲线 过点 ,交 于点 ,连接 , .若 , ,则 的值为( )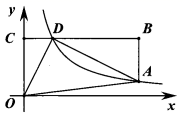 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
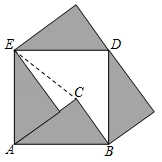
13. 计算: .14. 新冠肺炎疫情爆发以来,给全世界人民的生命安全,带来了很大的威胁,截至2020年12月10日,根据世界卫生组织统计,全球感染新冠肺炎的确诊病例超过19400000,请把数19400000用科学记数法表示为.15. 清代数学家梅文鼎在《勾股举隅》一书中,用四个全等的直角三角形拼出正方形 的方法证明了勾股定理(如图),若 的斜边 , ,则图中线段 的长为.
 16. 现将背面完全相同,正面分别标有数 ,1,2,3的四张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数标记为 ,再从剩下的三张卡片中任取一张,将该卡片上的数记为 ,则数字 、 都、不是方程 的解的概率为.17. 某天早晨,亮亮、悦悦两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,亮亮到达B地后立即以另一速度按原路返回.如图是两人离A地的距离y(米)与悦悦运动的时间x(分)之间的函数图象,则亮亮到达A地时,悦悦还需要分到达A地.
16. 现将背面完全相同,正面分别标有数 ,1,2,3的四张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数标记为 ,再从剩下的三张卡片中任取一张,将该卡片上的数记为 ,则数字 、 都、不是方程 的解的概率为.17. 某天早晨,亮亮、悦悦两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,亮亮到达B地后立即以另一速度按原路返回.如图是两人离A地的距离y(米)与悦悦运动的时间x(分)之间的函数图象,则亮亮到达A地时,悦悦还需要分到达A地.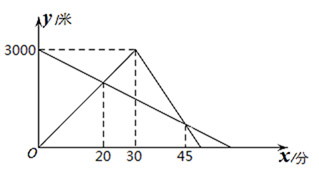 18. 如图,在边长为2的正方形 中,点 , 分别是边 , 上的动点,且 ,连接 , ,线段 和 相交于点 ,连接 ,取 的中点 ,连接 ,则线段 的最小值为.
18. 如图,在边长为2的正方形 中,点 , 分别是边 , 上的动点,且 ,连接 , ,线段 和 相交于点 ,连接 ,取 的中点 ,连接 ,则线段 的最小值为.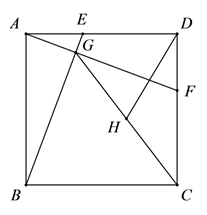
三、解答题
-
19. 解方程:(1)、 ;(2)、 .20. 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,点E是AB的中点,连结DE.
 (1)、求证:△ABD是等腰三角形;(2)、求∠BDE的度数.21. 某学校七年级、八年级各有500名学生,为了解两个年级的学生对垃圾分类知识的掌握情况,学校从七年级、八年级各随机抽取20名学生进行垃圾分类知识测试,满分100分,成绩整理分析过程如下,请补充完整:
(1)、求证:△ABD是等腰三角形;(2)、求∠BDE的度数.21. 某学校七年级、八年级各有500名学生,为了解两个年级的学生对垃圾分类知识的掌握情况,学校从七年级、八年级各随机抽取20名学生进行垃圾分类知识测试,满分100分,成绩整理分析过程如下,请补充完整:(收集数据)七年级20名学生测试成绩统计如下:
67,58,64,56,69,70,95,84,74,77,78,78,71,86,91,86,86,92,86,70
(整理数据)按照如下分数段整理、描述两组样本数据:
成绩
七年级
2
3
7
5
3
八年级
0
4
5
7
4
(分析数据)两组样本数据的平均数、中位数、众数、方差如下表所示:
年级
平均数
中位数
众数
方差
七年级
76.9
126.2
八年级
79.2
81
74
100.4
(1)、请直接写出 , 的值;(2)、根据抽样调查数据,估计七年级垃圾分类知识测试成绩在80分及其以上的大约有多少人?(3)、通过以上分析,你认为哪个年级对垃圾分类知识掌握得更好,并说明推断的合理性(说明两条理由即可).22. 阅读材料:材料一:对实数 , ,定义 的含义为:当 时, ;当 时, .例如: ; .
材料二:关于数学家高斯的故事:2000多年前,高斯的老师提出了下面的问题:
?据说,当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确答案: .
也可以这样理解:令 ①,
则 ②,
①+②得: ,
即 .
解决问题:
(1)、已知 ,且 ,求 的值;(2)、对于正数 ,满足关系式 时,求: 的值.
23. 某“数学兴趣小组”根据学习函数的经验,对函数 的图象和性质进行了探究,探究过程如下,请补充完整.(1)、如图,在平面直角坐标系 中,请同学们自己列表并画出函数图象;
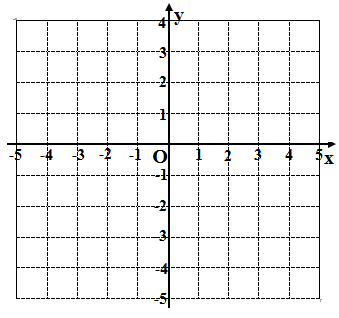 (2)、根据函数图象,写出该函数的两条性质:
(2)、根据函数图象,写出该函数的两条性质:①
②
(3)、若关于 的方程 有两个互不相等的实数根,则实数 的取值范围是.24. 2020年,中央全面落实“稳房价”的长效管控机制,重庆房地产市场较上一年成功稳定并略有回落.11月, 地产共推出花园洋房和小高层两种房型共80套,其中花园洋房每套面积200平方米,单价2万元/平方米,小高层每套面积100平方米,单价1.8万元/平方米:(1)、 地产11月的销售总额为18800万元,则11月 地产要推出多少套花园洋房?(2)、2020年12月,中央经济会议上重申“房子是拿来住的,不是拿来炒的”.重庆积极响应会议精神, 地产调整营销方案,12月推出两种房型的总数量仍为80套,并将花园洋房的单价在原有基础上每平方米下调 万元 ,将小高层的单价在原有基础上每平方米下调 万元,这样花园洋房的销量较(1)中11月的销量上涨了 套,且推出的房屋全部售罄,结果12月的销售总额比(1)中11月的销售总额少了290万元.求 的值.25. 如图1,已知抛物线 的顶点坐标为 ,与 轴分别交于 , 两点,与 轴交于 点,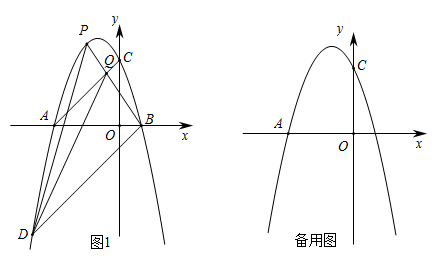 (1)、求该抛物线的解析式;(2)、如图1,连接 ,过 作 交抛物线于点 .点 为线段 上方抛物线上的一个动点,连接 交 于点 ,连接 , .当 面积最大时,求此时点 的坐标及 面积的最大值;(3)、将抛物线沿水平方向平移一定的距离,平移后的抛物线的顶点为 ,在平面直角坐标系中,是否存在一点 ,使以点 , , , 为顶点且以线段 为边的四边形为菱形,若存在,请直接写出点 的坐标;若不存在,请说明理由.26. 如图,在等腰 中, ,点 , 分别在 , 上运动,将线段 绕点 按顺时针方向旋转90°得到线段 .(1)、如图1,若 为 中点,点 与点 重合, 与 相交于点 ,求证: ;
(1)、求该抛物线的解析式;(2)、如图1,连接 ,过 作 交抛物线于点 .点 为线段 上方抛物线上的一个动点,连接 交 于点 ,连接 , .当 面积最大时,求此时点 的坐标及 面积的最大值;(3)、将抛物线沿水平方向平移一定的距离,平移后的抛物线的顶点为 ,在平面直角坐标系中,是否存在一点 ,使以点 , , , 为顶点且以线段 为边的四边形为菱形,若存在,请直接写出点 的坐标;若不存在,请说明理由.26. 如图,在等腰 中, ,点 , 分别在 , 上运动,将线段 绕点 按顺时针方向旋转90°得到线段 .(1)、如图1,若 为 中点,点 与点 重合, 与 相交于点 ,求证: ;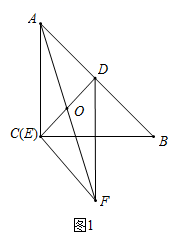 (2)、如图2,若点 不与 , 重合,点 为 中点,点 为 的中点,连接 ,连接 ,判断线段 , , 的数量关系并说明理由;
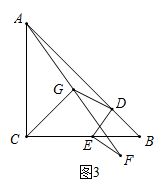
(2)、如图2,若点 不与 , 重合,点 为 中点,点 为 的中点,连接 ,连接 ,判断线段 , , 的数量关系并说明理由;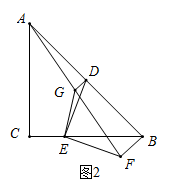 (3)、如图3,若 , ,点 为 的中点,连接 , ,请直接写出 的长.
(3)、如图3,若 , ,点 为 的中点,连接 , ,请直接写出 的长.