浙江省杭州市拱墅区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 任意抛掷一枚均匀的骰子，骰子停止转动后，发生可能性最大的事件是（）

A、朝上一面的点数大于2 B、朝上一面的点数为3 C、朝上一面的点数是2的倍数 D、朝上一面的点数是3的倍数

查看试题解析
2. 若二次函数 $y = a x^{2} (a \neq 0)$ 的图象过点 $(- 2, - 3)$ ，则必在该图象上的点还有（）

A、 $(- 3, - 2)$ B、 $(2, 3)$ C、 $(2, - 3)$ D、 $(- 2, 3)$

查看试题解析
3. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A C = 4$ ， $B C = 3$ ，则（）

A、 $\sin A = \frac{3}{4}$ B、 $\cos A = \frac{4}{5}$ C、 $\cos B = \frac{3}{4}$ D、 $\tan B = \frac{3}{5}$

查看试题解析
4. 若四边形ABCD是圆内接四边形，则它的内角 $∠ A$ ， $∠ B$ ， $∠ C$ ， $∠ D$ 的度数之比可能是（）

A、3：1：2：5 B、1：2：2：3 C、2：7：3：6 D、1：2：4：3

查看试题解析
5. 在10倍的放大镜下看到的三角形与原三角形相比，三角形的周长（）

A、没有发生变化 B、放大了10倍 C、放大了30倍 D、放大了100倍

查看试题解析
6. 如图，在 $⊙ O$ 中，弦AC与半径OB交于点D，连接OA，BC.若 $∠ B = 60 °$ ， $∠ A D B = 116 °$ ，则 $∠ A O B$ 的度数为（）

A、132° B、120° C、112° D、110°

查看试题解析
7. 已知 $(- 3 ， y_{1})$ ， $(- 2 ， y_{2})$ ， $(1 ， y_{3})$ 是二次函数 $y = - 2 x^{2} - 8 x + m$ 图象上的点，则（）

A、 $y_{2} > y_{1} > y_{3}$ B、 $y_{2} > y_{3} > y_{1}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
8. 如图，在 $△ A B C$ 中，点D在边AB上， $D E // B C$ 交AC于点E.连接BE， $D F // B E$ 交AC于点F.若 $A F = 3$ ， $C F = 5$ ，则 $△ D E F$ 与 $△ B D E$ 的面积之比为（）

A、 $\frac{3}{5}$ B、 $\frac{\sqrt{6}}{4}$ C、 $\frac{5}{8}$ D、 $\frac{\sqrt{15}}{6}$

查看试题解析
9. 如图， $A B$ 是 $⊙ O$ 的弦（非直径），点C是弦 $A B$ 上的动点（不与点A，B重合），过点C作垂直于 $O C$ 的弦 $D E$ .若设 $⊙ O$ 的半径为r，弦 $A B$ 的长为a， $\frac{A C}{B C} = m$ ，则弦 $D E$ 的长（）

A、与r，a，m的值均有关 B、只与r，a的值有关 C、只与r，m的值有关 D、只与a，m的值有关

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x - 1$ （a，b是常数， $a \neq 0$ ）的图象经过 $A (2 ， 1)$ ， $B (4 ， 3)$ ， $C (4 ， - 1)$ 三个点中的其中两个点.平移该函数的图象，使其顶点始终在直线 $y = x - 1$ 上，则平移后所得抛物线与y轴交点纵坐标的（）

A、最大值为 $- 1$ B、最小值为 $- 1$ C、最大值为 $- \frac{1}{2}$ D、最小值为 $- \frac{1}{2}$

查看试题解析

二、填空题

11. 由 $4 a = 7 b$ ，可得比例式：（写出一个正确的比例式即可）.

查看试题解析

12. 在同样条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表：

试验种子数n（粒）	1	5	50	100	200	500	1000	2000	3000
发芽频数m	1	4	45	92	188	476	952	1900	2850
发芽频率 $\frac{m}{n}$	1	0.8	0.9	0.92	0.94	0.952	0.952	0.95	0.95

估计该麦种的发芽概率约为.

查看试题解析

13. 如图，折扇的骨柄长为30cm，扇面宽度为18cm，折扇张开的角度为120°，则扇面外端 $\overset{⌢}{A B}$ 的长为cm，折扇扇面的面积为 ${cm}^{2}$ .（结果保留 $π$ ）

查看试题解析
14. 一个球从地面上竖直向上弹起时，距离地面的高度h（米）与经过的时间t（秒）满足的函数关系为 $h = 15 t - 5 t^{2}$ ，则该球从弹起至回到地面的时间需秒，它距离地面的最大高度为米.

查看试题解析
15. 如图是一可调节座椅的侧面示意图，靠背AO与地面垂直.为了使座椅更舒适，现调整靠背，把OA绕点O旋转到 $O A^{'}$ 处.若 $A O = m$ ， $∠ A O A' = α$ ，则调整后点 $A^{'}$ 比调整前点A的高度降低了（用含m， $α$ 的代数式表示）.

查看试题解析
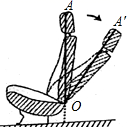16. 如图，在锐角三角形ABC中， $∠ B = 45 °$ ， $\frac{A B}{A C} = \frac{6}{5}$ ，点D为边AB的中点，点E在边AC上，将 $△ A D E$ 沿DE折叠得到 $△ F D E$ .若 $F E ⊥ A C$ ，则 $\frac{A E}{E C}$ 的值为； $\frac{D E}{A F}$ 的值为.

查看试题解析

三、解答题

17. 现有三张正面分别标有一个正数，一个负数和一个0的不透明卡片，它们除数字外其余完全相同，将它们背面朝上洗均匀.

(1)、从中随机抽取一张卡片，卡片上的数是0的概率为多少？

(2)、从中随机抽取一张卡片，记下数字后放回，背面朝上洗均匀，再随机抽取-张记下数字，求前后两次抽取的数字之积为0的概率.（用列表法或画树状图求解）

查看试题解析
18. 如图，小锋将一架4米长的梯子AB斜靠在竖直的墙AC上，使梯子与地面所成的锐角 $α$ 为60°.

(1)、求梯子的顶端与地面的距离AC（结果保留根号）

(2)、为使梯子顶端靠墙的高度更高，小锋调整了梯子的位置使其与地面所成的锐角 $α$ 为70°，则需将梯子底端点B向内移动多少米（结果精确到0.1米）？参考数据： $\sin 70 ° \approx 0.94$ ， $\cos 70 ° \approx 0.34$ ， $\tan 70 ° \approx 2.75$ .

查看试题解析
19. 已知二次函数 $y = (x + m) (x - 1)$ 的图象经过点 $(2 ， - 3)$ .

(1)、求这个二次函数的表达式；

(2)、画出这个函数的图象，并利用图象解决下列问题：
①直接写出方程 $(x + m) (x - 1) = - 3$ 的解；

②当x满足什么条件时， $y > 0$ .

查看试题解析
20. 如图，AB是 $⊙ O$ 的直径，四边形ABCD内接于 $⊙ O$ ，OD交AC于点E，AD=CD.

(1)、求证： $O D // B C$ ；

(2)、若 $A C = 10$ ， $D E = 4$ ，求BC的长.

查看试题解析
21. 如图，在四边形ABCD中，AC，BD相交于点E，点F在BD上，且 $∠ B A F = ∠ D B C$ ， $\frac{A B}{A F} = \frac{B C}{F D}$ .

(1)、求证： $△ A B C \sim △ A F D$ .

(2)、若 $A D = 2$ ， $B C = 5$ ， $△ A D E$ 的面积为20，求 $△ B C E$ 的面积.

查看试题解析
22. 在平面直角坐标系中，设二次函数 $y = a x^{2} + b x - 3 a$ （a，b是实数， $a \neq 0$ ）.

(1)、判断该函数图象与x轴的交点个数，并说明理由；

(2)、若该函数图象的对称轴为直线 $x = 1$ ， $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 为函数y图象上的任意两点，其中 $x_{1} < x_{2}$ .求当 $x_{1}$ ， $x_{2}$ 为何值时， $y_{1} = y_{2} = 5 a$ ；

(3)、若该函数图象的顶点在第二象限，且过点 $(1 ， 1)$ .当 $a < b$ 时，求 $2 a + b$ 的取值范围.

查看试题解析
23. 如图，在锐角三角形ABC中， $A B = A C$ ， $⊙ O$ 是 $△ A B C$ 的外接圆，连结AO，BO，延长BO交AC于点D.

(1)、求证：AO平分 $∠ B A C$ ；

(2)、若 $⊙ O$ 的半径为5， $A D = 6$ ，设 $△ A B O$ 的面积为 $S_{1}$ ， $△ B C D$ 的面积为 $S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的值；

(3)、若 $\frac{O D}{O B} = m$ ，求 $\cos ∠ B A C$ 的值（用含m的代数表示）.

查看试题解析