四川省眉山市东坡区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个实数中，最大的数是（）

A、﹣2 B、 $\sqrt{2}$ C、﹣1 D、0

查看试题解析
2. 下列对于二次根式的计算正确的是（）

A、 $\sqrt{5} + \sqrt{5} = \sqrt{10}$ B、 $2 \sqrt{5} － \sqrt{5} = 2$ C、 $2 \sqrt{5} \div \sqrt{5} = 2$ D、 $2 \sqrt{5} \times \sqrt{5} = \sqrt{50}$

查看试题解析
3. 在平面直角坐标系中，将点A（-1，2）向下平移3个单位长度，再向右平移2个单位长度，得到点A′，则点A′的坐标是（）

A、（-3，-1） B、（1，-1） C、（-1，1） D、（-4，4）

查看试题解析
4. 一个布袋里装有2个红球、3个黄球和5个白球，除颜色外其它都相同.搅匀后任意摸出一个球，是黄球的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{10}$ C、 $\frac{1}{5}$ D、 $\frac{7}{10}$

查看试题解析
5. 一元二次方程 ${(2 x + 1)}^{2} = 2 (2 x + 1)$ 的解是（）

A、 $x_{1} = x_{2} = \frac{1}{2}$ B、 $x_{1} = x_{2} = - \frac{1}{2}$ C、 $x_{1} = - \frac{1}{2}, x_{2} = \frac{1}{2}$ D、 $x_{1} = 1, x_{2} = \frac{1}{2}$

查看试题解析
6. 估计 $(2 \sqrt{2} + 4 \sqrt{3}) \times \sqrt{\frac{1}{2}}$ 的值应在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
7. 若关于x的一元二次方程 $x^{2} - 2 x + m = 0$ 有实数根，则实数m的取值范围是（）

A、m≥ 1 B、m＜1 C、m＞-1 D、m≤ 1

查看试题解析
8. 我市某楼盘准备以每平方9000元的均价对外销售，由于考虑经济受疫情影响，购房者持币观望，为了加快资金周转，房地产开发商对价格经过连续两次下调后，决定以每平方7290元的均价开盘销售，则平均每次下调的百分率是（）

A、9% B、8% C、10% D、11%

查看试题解析
9. 如图，在Rt△ABC中，∠ACB=90°，点D、E分别是AB、BC的中点，点F是BD的中点，若AB=5，则EF=（）

A、 $\frac{5}{4}$ B、 $\frac{5}{2}$ C、 $\frac{3}{2}$ D、2

查看试题解析
10. 古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点G将一线段MN分为两线段MG、GN，使得其中较长的一段MG是全长MN与较短的一段GN的比例中项，即满足 $\frac{M G}{M N} = \frac{G N}{M G} = \frac{\sqrt{5} - 1}{2}$ ，后人把 $\frac{\sqrt{5} - 1}{2}$ 这个数称为“黄金分割数”，把点G称为线段MN的“黄金分割点”.如图，在△ABC中，已知AB＝AC＝3，BC＝4，若点D是边BC边上的一个“黄金分割点”，则△ADC的面积为（）

A、 $5 - \sqrt{5}$ B、 $3 \sqrt{5} - 5$ C、 $20 - 8 \sqrt{5}$ D、 $10 - 4 \sqrt{5}$

查看试题解析
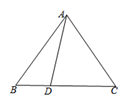11. 已知二次函数 $y = (x - a - 1) (x - a + 1) - 3 a + 7$ (其中 $x$ 是自变量)的图象与 $x$ 轴没有公共点，且当 $x < - 1$ 时， $y$ 随 $x$ 的增大而减小，则实数 $a$ 的取值范围是（）

A、 $a < 2$ B、 $a > - 1$ C、 $- 1 < a \leq 2$ D、 $- 1 \leq a < 2$

查看试题解析
12. 如图，E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点，连接AC、HE、EC、GA、GF，已知AG⊥GF，AC＝ $\sqrt{6}$ ，则下列结论：①∠DGA=∠CGF；②△DAG∽△CGF；③AB=2；④BE= $\sqrt{2}$ CF.正确的个数是（）

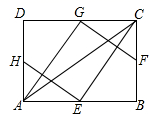A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

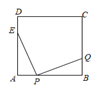
13. 要使二次根式 $\sqrt{x - 2} - \sqrt{2 - x}$ 有意义，则x的值是.

查看试题解析
14. 将二次函数 $y = x^{2}$ 的图象沿x轴向右平移2个单位，平移后的抛物线解析式是.

查看试题解析
15. 在△ABC中，∠C=90°，若tanA= $\frac{1}{2}$ ，则sinB= ．

查看试题解析
16. 已知m，n是方程 $x^{2} - 2 x - 1 = 0$ 的两实数根，则 $\frac{1}{m} + \frac{1}{n} =$ .

查看试题解析
17. 如图，正方形ABCD中，AD=4，AE=3DE，点P在AB上运动（不与A、B重合），过点P作PQ $⊥$ EP，交CB于点Q，则BQ的最大值是.

查看试题解析
18. 如图，抛物线 $y = a x^{2} + b x + c$ 的对称轴是x＝1，下列结论：①abc＞0；② $b^{2} - 4 a c > 0$ ；③8a+c＜0；④5a+b+2c＞0，正确的有（填序号）.

查看试题解析

三、解答题

19. 计算： $\sqrt{18} - 4 \cos 45 ° + {(1 - \sqrt{3})}^{0} - | - \sqrt{2} |$ .

查看试题解析
20. 解一元二次方程： $2 x^{2} - 3 x + 1 = 0$ .

查看试题解析
21. 如图，在△ABC中，BE平分∠ABC交AC于点E，过点E作ED∥BC交AB于点D.

(1)、求证：AE•BC＝BD•AC；

(2)、S_△_ADE＝4，S_四边形_BCED＝5，DE＝6，求BC的长.

查看试题解析
22. 知识改变世界，科技改变生活，中国北斗导航已经全球组网，走近人们的日常生活.如图，某校组织学生乘车到玉屏山（用C表示）开展研学实践活动，车到达A地后，发现C地恰好在A地的正南方向，且距离A地26千米，导航显示车辆应沿东南方向行驶至B地，再沿南偏西30°方向行驶一段距离才能到达C地，求B、C两地的距离.

查看试题解析
23. 为了解疫情期网学生网络学习的学习效果，东坡中学随机抽取了部分学生进行调查.要求每位学生从“优秀”、“良好”、“一般”、“不合格”四个等次中，选择一项作为自我评价网络学习的效果现将调查结果绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：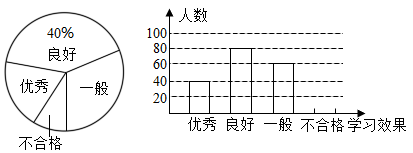

(1)、这次活动共抽查了人.

(2)、将条形统计图补充完整，并计算出扇形统计图中，学习效果“一般”的学生人数所在扇形的圆心角度数.

(3)、张老师在班上随机抽取了4名学生，其中学习效果“优秀”的1人，“良好”的2人，“一般”的1人，若再从这4人中随机抽取2人，请用画树状图法，求出抽取的2人学习效果全是“良好”的概率.

查看试题解析

24. 东坡区农产品资源极为丰富，其中晚熟柑橘远销北上广等大城市.某水果店购进一批优质晚熟柑橘，进价为5元/千克，售价不低于8元/千克，且不超过20元/每千克，根据销售情况，发现该柑橘在一天内的销售量y（千克）与该天的售价x（元/千克）之间的数量满足如下表所示的一次函数关系.

销售量y（千克）	…	42	45	48	51	…
售价x（元/千克）	…	18	15	12	9	…

(1)、某天这种柑橘售价为10元/千克.求当天该柑橘的销售量.

(2)、设某天销售这种柑橘获利m元，写出m与售价x之间的函数关系式.如果水果店该天获利450元，那么这天柑橘的售价为多少元？

查看试题解析

25. 在△ABC中，∠ACB＝90°，CD是中线，AC＝BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E、F，DF与AC交于点M，DE与BC交于点N.

(1)、如图，在∠EDF绕点D旋转的过程中，试证明CD²＝CE•CF恒成立；

(2)、若AB＝4，CF＝ $\sqrt{2}$ ，求DN的长.

查看试题解析
26. 如图所示，拋物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于A、B两点，与y轴交于点C，且点A的坐标为A（﹣2，0），点C的坐标为C（0，6），对称轴为直线x＝1.点D是抛物线上一个动点，设点D的横坐标为m（1＜m＜4），连接AC、BC、DC、DB.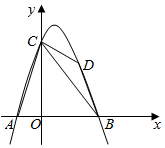

(1)、求抛物线的函数表达式；

(2)、当 $S △ B C D = \frac{3}{4} S △ A O C$ 时，求m的值；

(3)、在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B、D、M、N为顶点的四边形是平行四边形.若存在，请直接写出点M的坐标；若不存在，请说明理由.

查看试题解析