四川省乐山市犍为县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-02 类型:期末考试
一、单选题
-
1. 下列根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 ÷ D、3. 若 ,则 ( )A、 B、 C、 D、4. 用配方法解方程x2+4x+1=0,配方后的方程是( )A、(x﹣2)2=5 B、(x+2)2=5 C、(x+2)2=3 D、(x﹣2)2=35. Rt△ABC中,∠C=90°,AB=10,BC=6,则tanA=( )A、 B、 C、 D、6. 如图所示图案是我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为”赵爽弦图“.已知AE=4,BE=3,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为( )
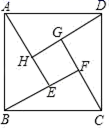 A、 B、 C、 D、7. 如图,二次函数 的图象经过点 , ,下列说法正确的是( )
A、 B、 C、 D、7. 如图,二次函数 的图象经过点 , ,下列说法正确的是( )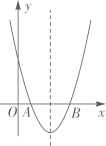 A、 B、 C、 D、图象的对称轴是直线8. 如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论错误的是( )
A、 B、 C、 D、图象的对称轴是直线8. 如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论错误的是( )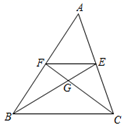 A、 B、 C、 D、9. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连 接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )
A、 B、 C、 D、9. 如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连 接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为( )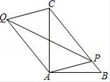 A、 B、 C、 D、210. 在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数 的图象上有且只有一个完美点 ,且当 时,函数 的最小值为﹣3,最大值为1,则m的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、210. 在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数 的图象上有且只有一个完美点 ,且当 时,函数 的最小值为﹣3,最大值为1,则m的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 当x时,二次根式 有意义.12. 一元二次方程 的根是 .13.
已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF= .
 14. 如图,在△ABC中,∠B=30°,AC=5,cosC= .则AB边的长为.
14. 如图,在△ABC中,∠B=30°,AC=5,cosC= .则AB边的长为.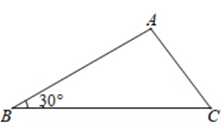 15. 形如 的根式叫做复合二次根式,对 可进行如下化简: = = +1,利用上述方法化简: =.16. 如图所示,有n+1个边长为1的等边三角形,点A、C1、C2、C3、…、Cn都在同一条直线上,若记△B1C1D1的面积为S1 , △B2C2D2的面积为S2 , △B3C3D3的面积为S3 , …,△BnCnDn的面积为Sn , 则(1)S1=;(2)Sn=.
15. 形如 的根式叫做复合二次根式,对 可进行如下化简: = = +1,利用上述方法化简: =.16. 如图所示,有n+1个边长为1的等边三角形,点A、C1、C2、C3、…、Cn都在同一条直线上,若记△B1C1D1的面积为S1 , △B2C2D2的面积为S2 , △B3C3D3的面积为S3 , …,△BnCnDn的面积为Sn , 则(1)S1=;(2)Sn=.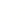
三、解答题
-
17. 计算: +( )-1﹣2cos30°﹣3 .18. 已知关于x的一元二次方程(m﹣3)x2﹣6x+m2﹣9=0的常数项为0,求m的值及此方程的解.19. 在平面直角坐标系中,已知抛物线y=x2﹣2x.(1)、它的顶点坐标是 , 当x时,y随x的增大而减小;(2)、将抛物线y=x2﹣2x向左平移2个单位长度,再向下平移3个单位长度,设所得新抛物线与x轴交于A、B两点,与y轴交于点C,写出新抛物线的解析式并求△ABC的面积.20. 在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)、“从中任意抽取1个球不是红球就是白球”是事件,“从中任意抽取1个球是黑球”是事件;(2)、从中任意抽取1个球恰好是红球的概率是;
(3)、学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
21. 已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2.(1)、求k的取值范围;(2)、若|x1+x2|=x1•x2﹣1,求k的值.22. “新冠”疫情蔓延全球,口罩成了人们的生活必需品,某药店销售普通口罩和N95口罩,今年3月份的进价如表:普通口罩
N95口罩
进价(元/包)
8
20
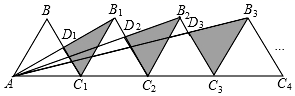
(1)、计划N95口罩每包售价比普通口罩售价贵16元,7包普通口罩和3包N95口罩总售价相同,求每包普通口罩和N95口罩的售价;(2)、按(1)中售价销售一段时间后,发现普通口罩的日均销售量为120包,当每包售价降价1元时,日均销售量增加20包,该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天的利润为320元,求此时普通口罩每包售价.23. 如图,在平行四边形ABCD中,点E是AC上一点,射线BE与CD的延长线交于点P,与边AD交于点F,连接FC.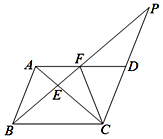 (1)、若∠ABF=∠ACF,求证:CE2=EF•EP;(2)、若点D是CP中点,BE=2 ,求EF的长.24. 如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C的仰角∠ADC=45°,从点E处看点B的仰角∠AEB=53°,且DE=2.4米.
(1)、若∠ABF=∠ACF,求证:CE2=EF•EP;(2)、若点D是CP中点,BE=2 ,求EF的长.24. 如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C的仰角∠ADC=45°,从点E处看点B的仰角∠AEB=53°,且DE=2.4米.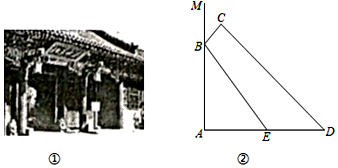 (1)、求点C到墙壁AM的距离;(2)、求匾额悬挂的高度AB的长.(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ )25. 如图,在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E,且E在AD上,BE交PC于点F.
(1)、求点C到墙壁AM的距离;(2)、求匾额悬挂的高度AB的长.(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ )25. 如图,在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E,且E在AD上,BE交PC于点F.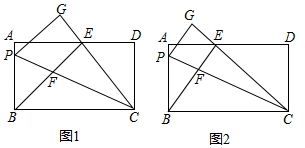 (1)、如图1,若点E是AD的中点,求证:△AEB≌△DEC;(2)、如图2,①求证:BP=BF;
(1)、如图1,若点E是AD的中点,求证:△AEB≌△DEC;(2)、如图2,①求证:BP=BF;②若AD=25,且AE DE,求AE的长和tan∠PCB的值;
③当BP=9时,直接写出BE•EF的值.
26. 如图,抛物线y=ax2+2x+c与x轴交于A、B两点,且与y轴交于点C(0,3),直线y=﹣x﹣1经过点A且与抛物线交于另一点D.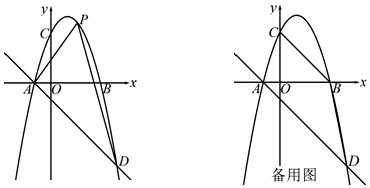 (1)、求抛物线的解析式;(2)、设点P是位于直线AD上方的抛物线上的一个动点,连接PA、PD,求△PAD的面积的最大值;(3)、Q点在x轴上且位于点B的左侧,若以Q,B,C为顶点的三角形与△ABD相似,求点Q的坐标.
(1)、求抛物线的解析式;(2)、设点P是位于直线AD上方的抛物线上的一个动点,连接PA、PD,求△PAD的面积的最大值;(3)、Q点在x轴上且位于点B的左侧,若以Q,B,C为顶点的三角形与△ABD相似,求点Q的坐标.