四川省成都市东部新区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列立体图形中，俯视图是三角形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在Rt△ABC中，∠C＝90°，AB＝4，sinA＝ $\frac{1}{2}$ ，则BC的长为（）

A、2 B、3 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
3. 一元二次方程 $x^{2} + x - 3 = 0$ 的根的情况是（）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、只有一个实数根

查看试题解析
4. 下列性质中，菱形具有而矩形不一定具有的是（）

A、对角线相等 B、对角线垂直 C、邻边垂直 D、邻角互补

查看试题解析
5. 若点A（ $- 1$ ， $y_{1}$ ），B（ $1$ ， $y_{2}$ ），C（ $2$ ， $y_{3}$ ）在反比例函数 $y = \frac{1}{x}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{3} > y_{1}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
6. 如图，在△ABC中，点D，E分别在边AB、AC上，下列条件中不能判断△ABC∽△ADE的是（）

A、∠ADE＝∠B B、∠AED＝∠C C、 $\frac{A D}{A E} = \frac{A B}{A C}$ D、 $\frac{D E}{B C} = \frac{A E}{A C}$

查看试题解析

7. 在一个不透明的口袋里，装有仅颜色不同的黑球和白球若干只，某小组做摸球实验：将球搅匀后从中随机摸出一个，记下颜色，再放入袋中，不断重复，下表是活动中的一组数据，则摸到白球的概率约是（）

摸球的次数 $n$	100	150	200	500	800	1000
摸到白球的次数 $m$	58	96	116	295	484	601
摸到白球的频率	0.58	0.64	0.58	0.59	0.605	0.601

A、0.5 B、0.55 C、0.6 D、0.65

查看试题解析

8. 某公司今年10月的营业额为2500万元，按计划12月的营业额要达到3600万元，求该公司11，12两个月营业额的月平均增长率.设该公司11，12两个月营业额的月平均增长率为x，则可列方程为（）

A、 $2500 {(1 + x)}^{2} = 3600$ B、 $3600 {(1 + x)}^{2} = 2500$ C、 $2500 (1 + 2 x) = 3600$ D、 $2500 (1 + x^{2}) = 3600$

查看试题解析
9. 如图，AB是⊙O的直径，点C，D在⊙O上，且∠BDC＝35°，则∠ABC的度数是（）

A、35° B、70° C、55° D、50°

查看试题解析
10. 关于二次函数 $y = 2 x^{2} - 4 x + 1$ ，下列说法正确的是（）

A、图象的对称轴在y轴左侧 B、图象的顶点在x轴下方 C、当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大 D、 $y$ 有最小值是1

查看试题解析

二、填空题

11. 若 $\frac{x}{y} = \frac{3}{2}$ ，则 $\frac{x - y}{y} =$ .

查看试题解析
12. 如图，四边形ABCD是一个正方形，E是BC延长线上一点，且AC＝EC，则∠DAE的度数为.

查看试题解析
13. 已知反比例函数 $y = \frac{m - 3}{x}$ 的图象具有下列特征：在所在的象限内，y随x的增大而增大，那么m的取值范围是.

查看试题解析
14. 如图所示是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影（圆形）的示意图.已知桌面的半径为0.8m，桌面距离地面1m，若灯泡距离地面3m，则地面上阴影部分的面积为m²（结果保留 $π)$ .

查看试题解析
15. 已知 $a$ ， $b$ 是方程 $x^{2} - x - 3 = 0$ 的两个实数根，则 $a^{2} + b + 1$ 的值为.

查看试题解析
16. 在Rt△ABC中，∠BCA＝90°，CD是AB边上的中线，BC＝8，CD＝5，则tan∠ACD＝ .

查看试题解析
17. 在平面直角坐标中，△ABC的顶点坐标分别是A（1，1），B（4，2），C（3，5），以点A为位似中心，相似比为1：2，把三角形ABC缩小，得到△AB₁C₁ ，则点C的对应点C₁的坐标为.

查看试题解析
18. 如图，平面直角坐标系xOy中，在反比例函数 $y = \frac{4 k}{x}$ （k＞0，x＞0）的图象上取点A，连接OA，与 $y = \frac{k}{x}$ 的图象交于点B，过点B作BC∥x轴交函数 $y = \frac{4 k}{x}$ 的图象于点C，过点C作CE∥y轴交函数 $y = \frac{k}{x}$ 的图象于点E，连接AC，OC，BE，OC与BE交于点F，则 $\frac{S_{Δ C E F}}{S_{Δ A B C}}$ ＝.

查看试题解析
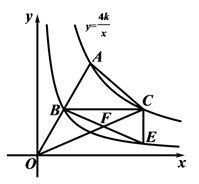19. 如图，在矩形ABCD中，AB＝4，BC＝ $4 \sqrt{3}$ ，M为BC边中点，E为AD边上的一动点，过点A作BE的垂线，垂足为F，连接FM，则FM的最小值为.在线段FM上取点G，使GM＝ $\frac{3}{4}$ FM，将线段GM绕点M顺时针旋转60°得到NM，连接GN，CN，则CN的最小值为.

查看试题解析

三、解答题

20.

(1)、计算： $2 \cos 45 ° - \sqrt{8} + | 1 - \sqrt{2} | - {(π + 3.14)}^{0}$

(2)、解方程： $x^{2} + 6 x + 8 = 0$

查看试题解析
21. 小明和小亮用如图所示的甲、乙两个转盘（甲转盘被分成五个面积相等的扇形，乙转盘被分成三个面积相等的扇形）做游戏，转动两个转盘各一次（如果指针恰好停在分割线上，那么重转一次，直到指针指向某一扇形区域为止）.

(1)、请求出甲转盘指针指向偶数区域的概率；

(2)、若两次数字之和为3，4或5时，则小明胜，否则小亮胜.这个游戏对双方公平吗？请用树状图或列表法说说你的理由.

查看试题解析
22. 如图，BD是△ABC的角平分线，过点D分别作BC和AB的平行线，交AB于点E，交BC于点F.

(1)、求证：四边形BEDF是菱形；

(2)、若AE＝3，BE＝4，求FC的长.

查看试题解析
23. 如图，某高为16.5米的建筑物AB楼顶上有一避雷针BC，在此建筑物前方E处安置了一高度为1.5米的测倾器DE，测得避雷针顶端的仰角为45°，避雷针底部的仰角为37°，求避雷针BC的长度.（参考数据： sin370≈0.60，cos370≈0.80，tan370≈0.75）

查看试题解析
24. 如图，在平面直角坐标系xOy中，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象都经过A（ $- 2$ ， $- 4$ ），B（4， $a$ ）两点.

(1)、求反比例函数和一次函数的表达式；

(2)、过O，A两点的直线与反比例函数图象交于点C，连接BC，求△ABC的面积.

查看试题解析
25. 如图，在Rt△ABC中，∠ACB=90°，点D在边AC上，∠DBC=∠BAC.⊙O经过A、B、D三点. 连接DO并延长交⊙O于点E，连接AE，DE与AB交于点F.

(1)、求证：CB是⊙O的切线；

(2)、求证：AB=EB；

(3)、若DF=3，EF=7，求BC的长.

查看试题解析
26. 某旅馆有客房120间，经市场调查发现，客房每天的出租数量 $y$ （间）与每间房的日租金 $x$ （元）的关系如图所示，为保证旅馆的收益，每天出租的房间数不少于90间.

(1)、结合图象，求出客房每天的出租的房间数 $y$ （间）与每间房的日租金 $x$ （元）之间的函数关系式和自变量的取值范围；

(2)、设客房的日租金总收入为 $W$ （元），不考虑其它因素，旅馆将每间客房的日租金定为多少元时，客房的日租金总收入最高？最高总收入为多少？

查看试题解析
27. 如图，在菱形ABCD中，AB＝ $2 \sqrt{13}$ ， $tan ∠ B A C = \frac{2}{3}$ . 点E在射线BC上，连接DE，DE绕点D顺时针旋转，旋转后得到的线段与对角线AC交于点F，旋转角∠EDF＝∠BAC.射线DE与射线AC交于点P.

(1)、如图1，当点E在线段BC上时，求证：△FDP∽△FCD.

(2)、如图2，点E在线段BC的延长线上，当DF＝5时，求线段CE的长.

(3)、如图3，连接EF，当 $E F / / A B$ 时，求线段EF的长.

查看试题解析
28. 如图1，在平面直角坐标xOy系中，已知抛物线y＝－ $\frac{1}{2}$ x²＋bx＋c与x轴交于点A（﹣4，0）、B（2，0），与y轴交于点C.

(1)、求抛物线的解析式；

(2)、如图2，沿直线AC平移抛物线y＝－ $\frac{1}{2}$ x²＋bx＋c，使得A、C两点的对应点E、F始终在直线AC上.
①设在平移过程中抛物线与y轴交于点M，求点M纵坐标的最大值；

②试探究抛物线在平移过程中，是否存在这样的点E，使得以A、E、B为顶点的三角形与△ABF相似.若存在，请求出此时点E的坐标；若不存在，请说明理由.

查看试题解析