江苏省无锡市滨湖区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程有实数根的是（）

A、x²＋x＋1＝0 B、x²－x－1＝0 C、x²－2x＋3＝0 D、x²－ $\sqrt{2}$ x＋1＝0

查看试题解析
2. 一个不透明的盒子中装有4个形状、大小质地完全相同的小球，这些小球上分别标有－1、0、2和3.从中随机摸取一个小球，则这个小球所标数字是正数的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
3. 对于一组数据－1，2，－1， 4，下列结论不正确的是（）

A、平均数是1 B、众数是－1 C、中位数是1.5 D、方差是4.5

查看试题解析
4. 抛物线y=（x＋2）²＋1的对称轴是（）

A、直线x＝－1 B、直线x＝1 C、直线x＝2 D、直线x＝－2

查看试题解析
5. 生活中到处可见黄金分割的美，如图，在设计人体雕像时，使雕像的腰部以下a与全身 $b$ 的高度比值接近0.618，可以增加视觉美感，若图中 $b$ 为2米，则a约为（）

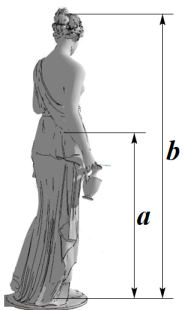A、1.24米 B、1.38米 C、1.42米 D、1.62米

查看试题解析
6. 如图是小刘做的一个风筝支架示意图，已知BC∥PQ，AB：AP=2：5，AQ=20cm，则CQ的长是（）

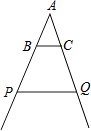A、8cm B、12cm C、30cm D、50cm

查看试题解析
7. 二次函数y=x²－(m－1)x+4的图象与x轴有且只有一个交点，则m的值为（）

A、1或－3 B、5或－3 C、－5或3 D、以上都不对

查看试题解析
8. 有一个三角形木架三边长分别是15cm，20cm，24cm，现要再做一个与其相似的三角形木架，而只有长为12cm和24cm的两根木条.要求以其中一根为一边，从另一根截下两段作为另两边（允许有余料），则不同的截法有（）

A、一种 B、两种 C、三种 D、四种

查看试题解析
9. 如图，在扇形BOC中，∠BOC＝60°，点D为弧BC的中点，点E为半径OB上一动点，若OB＝2，则阴影部分周长的最小值为（）

A、2＋ $\frac{π}{6}$ B、 $\frac{3}{2}$ $\sqrt{3}$ ＋ $\frac{π}{3}$ C、 $\frac{3}{2}$ $\sqrt{2}$ ＋ $\frac{π}{6}$ D、2 $\sqrt{2}$ ＋ $\frac{π}{3}$

查看试题解析
10. 已知二次函数y＝ax²＋bx＋c的顶点D（－1，2），与x轴的一个交点A在（－3，0）和（－2，0）之间（不含端点），如图所示，有以下结论：①b²－4ac＞0；②a＋b＋c＜0；③c－a＝2；④方程ax²＋bx＋c－2＝0有两个相等的实数根，其中结论正确的个数有（）

A、1个 B、2 个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知 $\frac{x}{y} = \frac{5}{2}$ ，则 $\frac{x - y}{y}$ ＝.

查看试题解析
12. 想了解中央电视台《开学第一课》的收视率，适合的调查方式为.（填“普查”或“抽样调查”）

查看试题解析
13. 某小区今年2月份绿化面积为6400m² ，到了今年4月份增长到8100m² ，假设绿化面积月平均增长率都相同，则增长率为．

查看试题解析
14. 若甲、乙、丙、丁4名同学3次数学成绩的平均分都是96分，它们的方差分别是S_甲²＝3.6，S_乙²＝4.6，S_丙²＝6.3 ，S_丁²＝7.3，则这4名同学3次数学成绩最稳定的是.

查看试题解析
15. 若圆锥的母线为10，底面半径为6，则圆锥的侧面积为．

查看试题解析
16. 设两直角边分别为3、4的直角三角形的外接圆和内切圆的半径长分别为R和r，则R—r =.

查看试题解析
17. 如图，C、D是半圆O上两点，AB是直径，若AD＝CD＝2，CB＝4，则半圆的半径为.

查看试题解析
18. 在平面直角坐标系xOy中，设点P的坐标为（n－1，3n＋2），点Q是抛物线y=－x²＋x＋1上一点，则P，Q两点间距离的最小值为.

查看试题解析

三、解答题

19. 解方程：

(1)、x²＋4x－1＝0；

(2)、x²＋10＝7x.

查看试题解析
20. 已知关于x的一元二次方程x²﹣6x+2m+1=0有实数根．

(1)、求实数m的取值范围；

(2)、若方程的两个实数根为x₁ ， x₂ ，且x₁x₂+x₁+x₂=15，求m的值．

查看试题解析
21. 甲、乙两个家庭准备到美丽的太湖景区游玩，各自随机选择到“灵山”、“拈花湾”、“鼋头渚”三个景点旅游.假设上述三个景点中的每一个景点被选到的可能性相同.

(1)、求甲家庭选择到“拈花湾”旅游的概率；

(2)、求甲、乙两个家庭选择到上述三个景点中的同一个景点旅游的概率.（用列表法或树状图法）

查看试题解析

22. 在新冠肺炎疫情期间，某市防控指挥部想了解各学校教职工参与志愿服务的情况.在全市各学校随机调查了部分参与志愿服务的教职工，对他们的志愿服务时间进行统计，整理并绘制成两幅不完整的统计图表.请根据两幅统计图表中的信息回答下列问题：

	志愿服务时间（小时）	频数
A	0＜x≤30	a
B	30＜x≤60	10
C	60＜x≤90	16
D	90＜x≤120	20

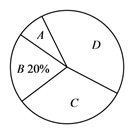(1)、本次被抽取的教职工共有名；

(2)、表中a＝，扇形统计图中“C”部分所占百分比为%；

(3)、扇形统计图中，“D”所对应的扇形圆心角的度数为°；

(4)、若该市共有30000名教职工参与志愿服务，那么志愿服务时间多于60小时的教职工大约有多少人？

查看试题解析

23. 如图，在边长为1小正方形的网格中，△ABC的顶点A、B、C均落在格点上，请用无刻度的直尺按要求作图.（保留画图痕迹，不需证明）

(1)、如图①，点P在格点上，在线段AB上找出所有符合条件的点Q，使△APQ和△ABC相似；

(2)、如图②，在AC上作一点M，使以M为圆心，MC为半径的⊙M与AB相切，并直接写出此时⊙M的半径为.

查看试题解析
24. 如图，在平行四边形ABCD中，∠ABC的平分线交AC于点E，交AD于点F，交CD的延长线于点G.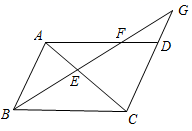

(1)、求证：△ABE∽△CGE；

(2)、若AF＝2FD，求 $\frac{B E}{E G}$ 的值.

查看试题解析
25. 如图，AB是⊙O的一条弦，点C是⊙O外一点， OC⊥OA，OC交AB于点P、交⊙O于点Q，且CP＝CB＝2.

(1)、求证：BC是⊙O的切线；

(2)、若∠A＝22.5°，求图中阴影部分的面积.

查看试题解析
26. 我区“绿色科技公司”研发了一种新产品，该产品的成本为每件3000元.在试销期间，营销部门建议：①购买不超过10件时，每件销售价为3600元；②购买超过10件时，每多购买一件，所购产品的销售单价均降低5元，但最低销售单价为3200元.根据以上信息解决下列问题：

(1)、直接写出：购买这种产品件时，销售单价恰好为3200元；

(2)、设购买这种产品x件（其中x＞10，且x为整数），该公司所获利润为y元，求y与x之间的函数表达式；

(3)、在试销期间销售人员发现：当购买产品的件数超过10件时，会出现随着数量的增多，公司所获利润反而减少这一情况.为使销售数量越多，公司所获利润越大，公司应将最低销售单价调整为多少元？（其它销售条件不变）

查看试题解析
27. 如图，平面直角坐标系xOy中，矩形OABC如图放置，点B（4，3），E，F分别为OA，BC边上的中点，动点P从点 $E$ 出发以每秒2个单位速度沿EO方向向点O运动，同时，动点Q从点F出发以每秒1个单位速度沿FB方向向点B运动.当一个点到达终点时，另一个点随之停止.连接EF、PQ，且EF与PQ相交于点M，连接AM.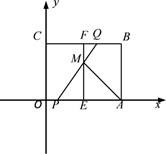

(1)、求线段AM的长度；

(2)、过点A作AH⊥PQ，垂足为点 $H$ ，连接CH，求线段CH长度的最小值.

查看试题解析
28. 已知二次函数y＝ax²－4ax＋c（a≠0）的图象与x轴的负半轴和正半轴分别交于A、B两点，与y轴交于点C，且△CAO和△BOC的面积之比为1∶3.

(1)、求A点的坐标；（直接写出答案）

(2)、若点C的坐标为（0，2c－2 ）.
①求二次函数的解析式；

②设点C关于x轴的对称点为C′，连接C′B，在线段C′B上是否存在一点P，使∠CPC′＝3∠CBO，若存在，求点P的坐标；若不存在，请说明理由.

查看试题解析