海南省省直辖县级行政单位澄迈县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-02 类型:期末考试
一、单选题
-
1. 下列是电视台的台标,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程中是关于 的一元二次方程的是( )A、 B、 C、 , D、3. 在平面直角坐标系中,点A(1,2)关于原点的对称点的坐标是( )A、(﹣2,﹣1) B、(﹣1,2) C、(1,﹣2) D、(﹣1,﹣2)4. 掷一枚质地均匀硬币,前3次都是正面朝上,掷第4次时正面朝上的概率是( )A、0 B、 C、 D、15. 下列成语所描述的事件是必然事件的是( )A、水涨船高 B、水中捞月 C、一箭双雕 D、拔苗助长6. 如果一个正多边形的中心角为60°,那么这个正多边形的边数是( )A、4 B、5 C、6 D、77. 某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是( )A、 B、 C、 D、8. 如图, 分别与 相切于 点,C为 上一点, ,则 ( )
2. 下列方程中是关于 的一元二次方程的是( )A、 B、 C、 , D、3. 在平面直角坐标系中,点A(1,2)关于原点的对称点的坐标是( )A、(﹣2,﹣1) B、(﹣1,2) C、(1,﹣2) D、(﹣1,﹣2)4. 掷一枚质地均匀硬币,前3次都是正面朝上,掷第4次时正面朝上的概率是( )A、0 B、 C、 D、15. 下列成语所描述的事件是必然事件的是( )A、水涨船高 B、水中捞月 C、一箭双雕 D、拔苗助长6. 如果一个正多边形的中心角为60°,那么这个正多边形的边数是( )A、4 B、5 C、6 D、77. 某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是( )A、 B、 C、 D、8. 如图, 分别与 相切于 点,C为 上一点, ,则 ( )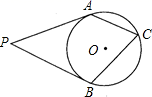 A、 B、 C、 D、9. 在二次函数 的图象中,若 随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、10.
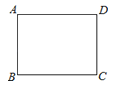
A、 B、 C、 D、9. 在二次函数 的图象中,若 随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、10.如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则下列各点中在⊙A外的是( )
 A、点A B、点B C、点C D、点D11. 定义运算:x*y=x2y﹣2xy﹣1,例如4*2=42×2﹣2×4×2﹣1=15,则方程x*1=0的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根12. 如图,A、B两点在双曲线y= 上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )
A、点A B、点B C、点C D、点D11. 定义运算:x*y=x2y﹣2xy﹣1,例如4*2=42×2﹣2×4×2﹣1=15,则方程x*1=0的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根12. 如图,A、B两点在双曲线y= 上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )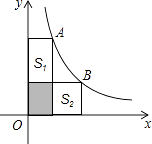 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
13. 已知反比例函数y= 图象经过第四象限的点(1,a)和(2,b),则a与b的大小关系是.14. 在一个不透明的盒子里装有除颜色外其余均相同的2个黄色乒乓球和若干个白色乒乓球,从盒子里随机摸出一个乒乓球,摸到白色乒乓球的概率为 ,那么盒子内白色乒乓球的个数为.15. 如图,将半径为2,圆心角为90°的扇形BAC绕点A逆时针旋转60°,点B、C的对应点分别为D、E,点D在 上,则阴影部分的面积为 .
 16. 抛物线 (a>0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,则a的取值范围是 .
16. 抛物线 (a>0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,则a的取值范围是 .三、解答题
-
17. 解下列方程:(1)、 ;(2)、 .18. 一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球,请用树状图或列表法求下列事件的概率.(1)、两次取出的小球的标号相同;(2)、两次取出的小球标号的和等于6.19. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(3,1)

( 1 )画出△ABC关于x轴对称的△A1B1C1 ,
( 2 )画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2 ,
( 3 )△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴.
20. 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图). (1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
(1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.