广西壮族自治区钦州市浦北县2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、等边三角形 B、矩形 C、正五边形 D、等腰梯形

查看试题解析
2. 下列方程中，是一元二次方程的为（）

A、x+2＝1 B、x+3y＝4 C、x²﹣5x＝0 D、x²+y＝2

查看试题解析
3. 在下列事件中，是随机事件的是（）

A、购买一张彩票，中奖 B、明天太阳从东方升起 C、通常加热到100℃时，水沸腾 D、任意画一个三角形，其内角和为360°

查看试题解析
4. 下列函数中是反比例函数的是（）

A、 $y = \frac{x}{2}$ B、y＝ $\frac{\sqrt{6}}{2 x}$ C、y＝﹣7x² D、y＝ $\frac{1}{x + 1}$

查看试题解析
5. 用配方法解方程x ²+2x﹣3＝0，下列配方结果正确的是（）

A、 ${(x - 1)}^{2} = 2$ B、 ${(x - 1)}^{2} = 4$ C、 ${(x + 1)}^{2} = 2$ D、 ${(x + 1)}^{2} = 4$

查看试题解析
6. 如图，将 $△ A B C$ 绕点B顺时针旋转 $60^{°}$ 得 $△ D B E$ ，点C的对应点E恰好落在AB的延长线上，连接AD.下列结论一定正确的是（）

A、 $∠ A B D = ∠ E$ B、 $∠ C B E = ∠ C$ C、AD=DE D、 $△ A D B$ 是等边三角形

查看试题解析
7. 不透明的袋子中装有2个红球，6个白球，这些球除了颜色外无其他差别.现从袋子中随机摸出1个球，则摸出的球是白球的概率为（）

A、 $\frac{3}{4}$ B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
8. 在直角坐标系中，把抛物线y＝x²+4向上平移2个单位长度，再向右平移3个单位长度，可得到抛物线的解析式为（）

A、y＝（x﹣3）²+2 B、y＝（x﹣3）²+6 C、y＝（x+3）²+2 D、y＝（x+3）²+6

查看试题解析
9. 如图，AB是⊙O的直径，∠AOC=110°，则∠D=（）

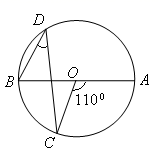A、25⁰ B、35⁰ C、55⁰ D、70⁰

查看试题解析
10. 惠多多超市2020年10月份的营业额为36万元，12月份的营业额为48万元.设该超市每月的平均增长率为x，则可列方程为（）

A、36（1+x）²＝48 B、36（1﹣x）²＝48 C、48（1+x）²＝36 D、48（1﹣x）²＝36

查看试题解析
11. 关于反比例函数 $y = \frac{2}{x}$ 的图象和性质，下列说法错误的是（）

A、函数图象关于原点对称 B、函数图象分别位于第一、三象限 C、点(﹣1，﹣2)在函数图象上 D、当x＞0时，y随x的增大而增大

查看试题解析
12.
如图，矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点（点P不与点B，C重合），现将△PCD沿直线PD折叠，使点C落下点C₁处；作∠BPC₁的平分线交AB于点E．设BP=x，BE=y，那么y关于x的函数图象大致应为（）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 一元二次方程3x²﹣x+9＝0的一次项是.

查看试题解析
14. 已知圆柱的体积是30cm² ，它的高h（单位：cm）关于底面面积S（单位：cm²）的函数解析式为.

查看试题解析
15. 把一副普通扑克牌中的13张黑桃牌洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的牌是黑桃4的概率是.

查看试题解析
16. 如图，若干全等正五边形排成环状．图中所示的是前3个五边形，要完成这一圆环还需个五边形．

查看试题解析
17. 如图，△ABC绕点A顺时针旋转45°得到△AB′C′，若∠BAC=90°，AB=AC=2 $\sqrt{2}$ ，则图中阴影部分的面积等于.

查看试题解析
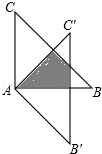18. 甲、乙两人进行羽毛球比赛，甲发出一颗十分关键的球，出手点为 $P$ ，羽毛球飞行的水平距离 $s$ （米）与其距地面高度 $h$ （米）之间的关系式为 $h = - \frac{1}{12} s^{2} + \frac{2}{3} s + \frac{3}{2}$ ，如图，已知球网 $A B$ 距原点 $5$ 米，乙（用线段 $C D$ 表示）扣球的最大高度为 $\frac{9}{4}$ 米，设乙的起跳点 $C$ 的横坐标为 $m$ ，若乙原地起跳，因球的高度高于乙扣球的最大高度而导致接球失败，则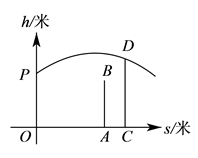 $m$ 的取值范围是.

查看试题解析

三、解答题

19. 解下列方程：

(1)、2x²﹣3x﹣5＝0；

(2)、（x+1）²＝6x+6.

查看试题解析
20. 已知一元二次方程（a﹣3）x²﹣4x+3＝0.

(1)、若方程的一个根为x＝﹣1，求a的值；

(2)、若方程有实数根，求满足条件的正整数a的值.

查看试题解析
21. 如图，在直角坐标系中，已知 $△$ ABC的三个顶点坐标分别为A(1，3)，B(4，2)，C(3，4).

（ 1 ）请画出 $△$ ABC关于原点O对称的 $△$ A₁B₁C₁；

（ 2 ）请画出 $△$ ABC绕点O逆时针旋转90°后的 $△$ A₂B₂C₂ ，并直接写出点B旋转到点B₂所经过的路径长.

查看试题解析
22. 为了方便业主合理、规范摆放机动车，小伟所住生活小区的管理人员在小区内部道路的一侧画出了一些停车位.如图，道路上有四个空停车位，标号分别为1，2，3，4，如果有两辆机动车要随机停在这四个停车位中的两个里边，请用列表或画树状图的方法求出这两辆机动车停在“标号是一个奇数和一个偶数”停车位的概率.

查看试题解析
23. 如图，D是等边三角形ABC内一点，将线段AD绕点A顺时针旋转60°，得到线段AE，连接CD，BE.

(1)、求证：EB=DC；

(2)、连接DE，若∠BED=50°，求∠ADC的度数.

查看试题解析
24. 如图，已知一次函数 $y = \frac{1}{2} x + b$ 的图象与反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象交于点A(-1，2)和点B.

(1)、求b和k的值；

(2)、请求出点B的坐标，并观察图象，直接写出关于x的不等式 $\frac{1}{2} x + b > \frac{k}{x}$ 的解集；

(3)、若点P在y轴上一点，当 $P A + P B$ 最小时，求点P的坐标.

查看试题解析
25. 如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点P，PD⊥AC于点D.

(1)、求证：PD是⊙O的切线；

(2)、若∠CAB=120°，AB=6，求BC的长.

查看试题解析
26.
已知如图，在平面直角坐标系xOy中，点A、B、C分别为坐标轴上上的三个点，且OA=1，OB=3，OC=4，

(1)、求经过A、B、C三点的抛物线的解析式；

(2)、在平面直角坐标系xOy中是否存在一点P，使得以以点A、B、C、P为顶点的四边形为菱形？若存在，请求出点P的坐标；若不存在，请说明理由；

(3)、若点M为该抛物线上一动点，在（2）的条件下，请求出当|PM﹣AM|的最大值时点M的坐标，并直接写出|PM﹣AM|的最大值．

查看试题解析