甘肃省金昌市联考2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列垃圾分类标识的图案既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 关于x的一元二次方程 $(k - 1) x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则k的取值范围是（）

A、k＞2 B、k＜2且k≠0 C、k＜2且k≠1 D、k＜2

查看试题解析
3. 将抛物线 $y = 2 x^{2}$ 向右平移1个单位，再向下平移3个单位得到的抛物线表达式是（）

A、 $y = 2 {(x + 1)}^{2} + 3$ B、 $y = 2 {(x - 1)}^{2} - 3$ C、 $y = 2 {(x - 1)}^{2} + 3$ D、 $y = 2 {(x + 1)}^{2} - 3$

查看试题解析
4. 如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连结BC．若∠A=36°，则∠C=（）

A、54° B、36° C、27° D、20°

查看试题解析
5. 在△ABC中，I是内心，∠BIC=130°，则∠A的度数是（）

A、40° B、50° C、65° D、80°

查看试题解析
6. 下列事件是必然事件的是（）

A、某人体温是100℃ B、三角形的内角和等于180度 C、购买一张彩票中奖 D、经过有交通信号灯的路口，遇到红灯

查看试题解析
7. 对于反比例函数 $y = \frac{2}{x}$ ，下列说法不正确的是（　　）

A、点（﹣2，﹣1）在它的图象上 B、它的图象在第一、三象限 C、当x＞0时，y随x的增大而增大 D、当x＜0时，y随x的增大而减小

查看试题解析
8.
如图，△OAB绕点O逆时针旋转80°到△OCD的位置，已知∠AOB=45°，则∠AOD等于（）

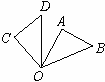A、35° B、40° C、45° D、55°

查看试题解析
9.
“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）。小亮同学随机地在大正方形及其内部区域投针，若直角三角形的两条直角边的长分别是2和1，则针扎到小正方形（阴影）区域的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
10. 在同一坐标系中， $y = k x - k$ 与 $y = \frac{k}{x} (k \neq 0)$ 的图象大致是（）

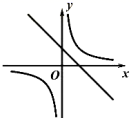A、 B、 C、 D、

查看试题解析

二、填空题

11. 三角形的两边长为4和6，第三边长是方程x²﹣6x+8=0的根，则该三角形的周长为.

查看试题解析
12. 某药品经过两次降价，每瓶零售价由100元降为81元.已知两次降价的百分率相同，则每次降价的百分率是.

查看试题解析
13. 钟表的分针长10cm，经过20分钟，它的针尖转过的弧长是cm.

查看试题解析
14. 一张扇形纸片，半径是6，圆心角为120°，将它围成一个圆锥，则这个圆锥的底面半径为.

查看试题解析
15. 如图是一圆形水管的截面图，已知⊙O的半径OA＝13，水面宽AB＝24，则水的深度CD是.

查看试题解析
16. 抛物线y=ax²+bx+c的部分图象如图所示，若y＞0，则x的取值范围是.

查看试题解析
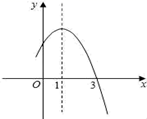17. 如图所示，设A为反比例函数 $y = \frac{k}{x}$ 图象上一点，且矩形ABOC的面积为3，则这个反比例函数解析式为.

查看试题解析
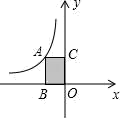18. 如图，在直角坐标系中，已知点A(－3，0)，B(0，4)，对△OAB连续作旋转变换，依次得到三角形①，②，③，④，…，则三角形⑩的直角顶点的坐标为.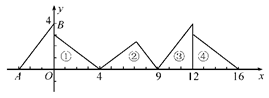

查看试题解析

三、解答题

19. 解方程

(1)、 $3 x^{2} - 5 x - 2 = 0$ ；

(2)、 $3 x (x - 1) = 2 (1 - x)$ .

查看试题解析
20.
如图，正方形网格中，△ABC为格点三角形（顶点都是格点），将△ABC绕点A按逆时针方向旋转90°得到△AB₁C₁ ．

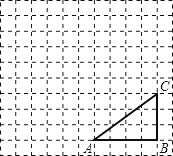
(1)、在正方形网格中，作出△AB₁C₁；（不要求写作法）

(2)、设网格小正方形的边长为1cm，用阴影表示出旋转过程中线段BC所扫过的图形，然后求出它的面积．（结果保留π）．

查看试题解析
21. 如图，在Rt△ABC中，∠C＝90°，

(1)、求作⊙P，使圆心P在BC上，且⊙P与AC、AB都相切；(要求：尺规作图，不写作法，保留作图痕迹)

(2)、在（1）的条件下，若AC＝4，BC＝3.求⊙P的半径.

查看试题解析
22. 在一个不透明的布袋里装有4个标号为1，2，3，4的小球，它们的形状、大小完全相同，小凯同学从布袋里随机取出一个小球，记下数字为x，小敏同学从剩下的3个小球中随机取出一个小球，记下数字为y，这样确定了点P的坐标（x，y）.

(1)、请你运用画树状图或列表的方法，写出点P所有可能的坐标；

(2)、求点P（x，y）在函数 $y = - x^{2} + 5$ 图象上的概率.

查看试题解析
23. 文具店某种文具进价为每件20元，市场调查反映：当售价为每件30元时，平均每星期可售出140件；而当每件售价涨1元，平均每星期少售出10件，设每件涨价 $x$ 元，平均每星期的总利润为 $y$ 元.

(1)、写出 $y$ 与 $x$ 的函数关系式，并求出自变量的取值范围；

(2)、如何定价才能使每星期的利润最大？且每星期的最大利润是多少？

查看试题解析
24. 如图，已知AB为⊙O的直径，CD是弦，且AB $⊥$ CD于点E。连接AC、OC、BC。

(1)、求证： $∠$ ACO= $∠$ BCD。

(2)、若EB= $8 cm$ ，CD= $24 cm$ ，求⊙O的直径。

查看试题解析
25. 如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点P，PD⊥AC于点D.

(1)、求证：PD是⊙O的切线；

(2)、若∠CAB=120°，AB=6，求BC的长.

查看试题解析
26. 如图，一次函数y=-x+3的图象与反比例函数 $y = \frac{k}{x}$ （k≠0），在第一象限的图象交于A（1，a）和B两点，与 $x$ 轴交于点C.

(1)、求出反比例函数的解析式；

(2)、求出△AOB的面积.

(3)、根据图象，直接写出在第一象限内，使一次函数值大于反比例函数值的x的取值范围.

查看试题解析
27. 如图，抛物线y=x²+bx+c与x轴交于A（﹣1，0）和B（3，0）两点，交y轴于点E.

(1)、求此抛物线的解析式.

(2)、求该抛物线的顶点坐标和对称轴；

(3)、若直线y=x+1与抛物线交于A、D两点，与y轴交于点F，连接DE，求△DEF的面积.

查看试题解析