福建省福州市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-02 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,是确定性事件的是( )A、篮球队员在罚球线上投篮一次,未投中 B、经过有交通信号灯的路口,遇到绿灯 C、投掷一枚骰子(六个面分别刻有 到 的点数),向上一面的点数大于 D、任意画一个三角形,其外角和是3. 将点 绕原点顺时针旋转 得到的点的坐标是( )A、 B、 C、 D、4. 已知正六边形 内接于 ,若 的直径为 ,则该正六边形的周长是( )A、 B、 C、 D、5. 已知甲,乙两地相距 (单位: ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间 (单位: )关于行驶速度 (单位: )的函数图象是( )A、
2. 下列事件中,是确定性事件的是( )A、篮球队员在罚球线上投篮一次,未投中 B、经过有交通信号灯的路口,遇到绿灯 C、投掷一枚骰子(六个面分别刻有 到 的点数),向上一面的点数大于 D、任意画一个三角形,其外角和是3. 将点 绕原点顺时针旋转 得到的点的坐标是( )A、 B、 C、 D、4. 已知正六边形 内接于 ,若 的直径为 ,则该正六边形的周长是( )A、 B、 C、 D、5. 已知甲,乙两地相距 (单位: ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间 (单位: )关于行驶速度 (单位: )的函数图象是( )A、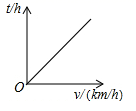 B、
B、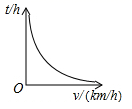 C、
C、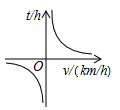 D、
D、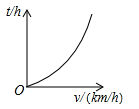 6. 已知二次函数 ,下列叙述中正确的是( )A、图象的开口向上 B、图象的对称轴为直线 C、函数有最小值 D、当 时,函数值 随自变量 的增大而减小7. 若关于 的方程 有两个不相等的实数根,则 的取值范围是( )A、 B、 且 C、 D、 且8. 如图, , 与 相交于点 ,若 , , ,则 的值是( )
6. 已知二次函数 ,下列叙述中正确的是( )A、图象的开口向上 B、图象的对称轴为直线 C、函数有最小值 D、当 时,函数值 随自变量 的增大而减小7. 若关于 的方程 有两个不相等的实数根,则 的取值范围是( )A、 B、 且 C、 D、 且8. 如图, , 与 相交于点 ,若 , , ,则 的值是( ) A、 B、 C、 D、9. 某餐厅主营盒饭业务,每份盒饭的成本为 元.若每份盒饭的售价为 元,每天可卖出 份.市场调查反映:如调整价格,每涨价 元,每天要少卖出 份.若该餐厅想让每天盒饭业务的利润达到 元,设每份盒饭涨价 元,则符合题意的方程是( )A、 B、 C、 D、10. 已知抛物线 ,抛物线与 轴交于 , 两点 ,则 , , , 的大小关系是( )A、 B、 C、 D、
A、 B、 C、 D、9. 某餐厅主营盒饭业务,每份盒饭的成本为 元.若每份盒饭的售价为 元,每天可卖出 份.市场调查反映:如调整价格,每涨价 元,每天要少卖出 份.若该餐厅想让每天盒饭业务的利润达到 元,设每份盒饭涨价 元,则符合题意的方程是( )A、 B、 C、 D、10. 已知抛物线 ,抛物线与 轴交于 , 两点 ,则 , , , 的大小关系是( )A、 B、 C、 D、二、填空题
-
11. 若 的半径为 ,则 的圆心角所对的弧长是.12. 若 是关于 的方程 的一个解,则 的值是.13. 已知反比例函数y= ,当-3<x<-1时,y的取值范围是.14. 如图,将一块等腰直角三角尺的锐角顶点 放在以 为直径的半圆 上, 的两边分别交半圆 于 , 两点,若 ,则 的长是.
 15. 《易经》是中华民族聪明智慧的结晶.如图是《易经》中的一种卦图,每一卦由三根线组成(线形为“
15. 《易经》是中华民族聪明智慧的结晶.如图是《易经》中的一种卦图,每一卦由三根线组成(线形为“ ”或“━”),如正北方向的卦为“
”或“━”),如正北方向的卦为“  ”.从图中任选一卦,这一卦中恰有 根“━”和 根“
”.从图中任选一卦,这一卦中恰有 根“━”和 根“  ”的概率是.
”的概率是.  16. 如图,在平行四边形 中, , , ,点 , 分别在边 , 上运动,且满足 ,连接 , ,则 的最小值是.
16. 如图,在平行四边形 中, , , ,点 , 分别在边 , 上运动,且满足 ,连接 , ,则 的最小值是.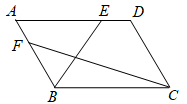
三、解答题
-
17. 解方程:18. 如图, 是 的直径, 为半圆 上一点,直线 经过点 ,过点 作 于点 ,连接 ,当 平分 时,求证:直线 是 的切线.
 19. 一名男生推铅球,铅球行进高度 (单位: )与水平距离 (单位: )之间的函数关系是 .如图, , 是该函数图象上的两点.
19. 一名男生推铅球,铅球行进高度 (单位: )与水平距离 (单位: )之间的函数关系是 .如图, , 是该函数图象上的两点. (1)、画出该函数的大致图象;(2)、请判断铅球推出的距离能否达到 ,并说明理由.20. 为发展学生多元能力,某校九年级开设 , , , 四门校本选修课程,要求九年级每个学生必须选报且只能选报其中一门.图 ,图 是九年(1)班学生 , , , 四门校本选修课程选课情况的不完整统计图.请根据图中信息,解答下列问题.
(1)、画出该函数的大致图象;(2)、请判断铅球推出的距离能否达到 ,并说明理由.20. 为发展学生多元能力,某校九年级开设 , , , 四门校本选修课程,要求九年级每个学生必须选报且只能选报其中一门.图 ,图 是九年(1)班学生 , , , 四门校本选修课程选课情况的不完整统计图.请根据图中信息,解答下列问题.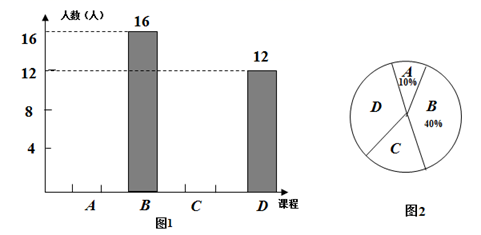 (1)、求九年(1)班学生的总人数及该班选报 课程的学生人数;(2)、在统计的信息中,我们发现九年(1)班的甲同学和乙同学选报了 课程,若从该班选报 课程的同学中随机抽取 名进行选修学习效果的测评,求甲,乙同时被抽中的概率.21. 如图,点 是等边三角形 内一点,连接 , ,将 绕点 顺时针旋转 ,点 的对应点为 .
(1)、求九年(1)班学生的总人数及该班选报 课程的学生人数;(2)、在统计的信息中,我们发现九年(1)班的甲同学和乙同学选报了 课程,若从该班选报 课程的同学中随机抽取 名进行选修学习效果的测评,求甲,乙同时被抽中的概率.21. 如图,点 是等边三角形 内一点,连接 , ,将 绕点 顺时针旋转 ,点 的对应点为 . (1)、画出旋转后的图形;(2)、当 , , 三点共线时,求 的度数.22. 如图,一次函数 的图象与 轴正半轴交于点 ,与反比例函数 的图象交于 , 两点,若 ,点 的纵坐标为 .
(1)、画出旋转后的图形;(2)、当 , , 三点共线时,求 的度数.22. 如图,一次函数 的图象与 轴正半轴交于点 ,与反比例函数 的图象交于 , 两点,若 ,点 的纵坐标为 . (1)、求反比例函数的解析式;(2)、求 的面积.23. 如图, ,作 ,使得点 , 在 异侧,且 , , 是 延长线上一点,连接 交 于点 .
(1)、求反比例函数的解析式;(2)、求 的面积.23. 如图, ,作 ,使得点 , 在 异侧,且 , , 是 延长线上一点,连接 交 于点 . (1)、求证: ;(2)、若 ,试判断 的形状,并说明理由.
(1)、求证: ;(2)、若 ,试判断 的形状,并说明理由.

