浙江省湖州市长兴县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-02 类型:期末考试
一、单选题
-
1. 二次函数 的顶点坐标是( )A、 B、 C、 D、2. 已知 的半径为5,若 ,则点 与 的位置关系是( )A、点 在 内 B、点 在 外 C、点 在 上 D、无法判断3. 某十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率为( )A、 B、 C、 D、4. 在 中, , , ,则 的值是( )A、 B、 C、 D、5. 一个扇形的圆心角是 ,半径是 ,那么这个扇形的面积是( )A、 B、 C、 D、6. 如图, 是 的直径,点 , 在 上.若 ,则 的度数是( )
 A、 B、 C、 D、7. 如图, , 分别是 两条中线,连结 ,则 的比值是( )
A、 B、 C、 D、7. 如图, , 分别是 两条中线,连结 ,则 的比值是( ) A、 B、 C、 D、8. 函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是( )
A、 B、 C、 D、8. 函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是( )
A、x<﹣4或x>2 B、﹣4<x<2 C、x<0或x>2 D、0<x<29. 如图,将 沿着过 中点 的直线折叠,使点 落在 边上的 处,称为第1次操作,折痕 到 的距离记为 ;还原纸片后,再将 沿着过 中点 的直线折叠,使点 落在 边上的 处,称为第2次操作,折痕 到 的距离记为 ;按上述方法不断操作下去,经过第4次操作后得到的折痕 到 的距离记为 ,若 ,则 的值是( ) A、 B、 C、 D、10. 如图, 中, , , , 是 的外接圆,点 是优弧 上任意一点(不包括点 , ),记四边形 的周长为 , 的长为 ,则 关于 的函数关系式是( )
A、 B、 C、 D、10. 如图, 中, , , , 是 的外接圆,点 是优弧 上任意一点(不包括点 , ),记四边形 的周长为 , 的长为 ,则 关于 的函数关系式是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若2a=3b,则a:b=.12. 已知 是 的弦, , 于点C, ,则 的半径是 .13. 一运动员乘雪橇以10米/秒的速度沿坡比 的斜坡匀速滑下,若下滑的垂直高度为1000米,则该运动员滑到坡底所需的时间是秒.14. 在1,2,3三个数中任取两个不同的数,组成一个两位数,则组成的两位数是偶数的概率是.15. 如图,已知在 中, , , ,点 在边 上,将 沿着过点 的一条直线翻折,使点 落在边 上的点 处,连结 , ,若 ,则 的长是.
 16. 如图,在 中,点 为弧 的中点,弦 , 互相垂直,垂足为 , 分别与 , 相于点 , ,连结 , .若 的半径为2, 的度数为 ,则线段 的长是.
16. 如图,在 中,点 为弧 的中点,弦 , 互相垂直,垂足为 , 分别与 , 相于点 , ,连结 , .若 的半径为2, 的度数为 ,则线段 的长是. 17. 计算:2sin30°+tan45°= .
17. 计算:2sin30°+tan45°= .三、解答题
-
18. 已知等边三角形 (如图).
 (1)、用直尺和圆规作 的外接圆(不写作法,保留作图痕迹).(2)、若 ,求 的外接圆半径.19. 如图,在 中, ,以 为直径的 交 于点 ,交 于点 ,连结 , .
(1)、用直尺和圆规作 的外接圆(不写作法,保留作图痕迹).(2)、若 ,求 的外接圆半径.19. 如图,在 中, ,以 为直径的 交 于点 ,交 于点 ,连结 , .
求证:
(1)、点D是 的中点.(2)、 .20. 一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同。
(1)、求摸出1个球是白球的概率;
(2)、摸出1个球,记下颜色后放回,并搅均,再摸出1个球。求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)、现再将n个白球放入布袋,搅均后,使摸出1个球是白球的概率为。求n的值。
21. 某兴趣小组借助无人飞机航拍校园,如图,无人飞机从 处平行飞行至 处需10秒,在地面 处同一方向上分别测得 处的仰角为 , 处的仰角为 ,已知无人飞机的飞行速度为5米/秒,求这架无人飞机的飞行高度(结果保留根号). 22. 如图,在平面直角坐标系中,已知 , , ,点 的坐标为 .
22. 如图,在平面直角坐标系中,已知 , , ,点 的坐标为 .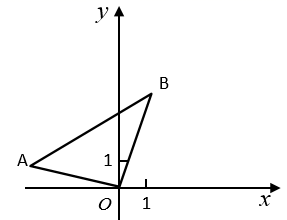 (1)、求点 的坐标.(2)、求过点 , , 的二次函数的表达式.(3)、设点 关于二次函数的对称轴 的对称点为 ,求 的面积.23. 如图,在矩形 中, , ,点 是对角线 上的一个动点,过点 作 ,交边 于点 (点 与点 , 都不重合),点 是射线 上一动点,连结 , ,并一直保持 .
(1)、求点 的坐标.(2)、求过点 , , 的二次函数的表达式.(3)、设点 关于二次函数的对称轴 的对称点为 ,求 的面积.23. 如图,在矩形 中, , ,点 是对角线 上的一个动点,过点 作 ,交边 于点 (点 与点 , 都不重合),点 是射线 上一动点,连结 , ,并一直保持 .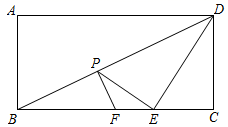 (1)、求证: .(2)、设 的长为 , 的面积为 ,求 关于 的函数表达式,并写出自变量 的取值范围.(3)、当 与 相似时,求 的面积.24. 如图,在平面直角坐标系中,二次函数 的图象经过 , 两点,且与 轴交于点 .点 为 轴负半轴上一点,且 ,点 , 分别在线段 和 上.
(1)、求证: .(2)、设 的长为 , 的面积为 ,求 关于 的函数表达式,并写出自变量 的取值范围.(3)、当 与 相似时,求 的面积.24. 如图,在平面直角坐标系中,二次函数 的图象经过 , 两点,且与 轴交于点 .点 为 轴负半轴上一点,且 ,点 , 分别在线段 和 上. (1)、求这个二次函数的表达式.(2)、若线段 被 垂直平分,求 的长.(3)、在第一象限的这个二次函数的图象上取一点 ,使得 ,再在这个二次函数的图象上取一点 (不与点 , , 重合),使得 ,求点 的坐标.
(1)、求这个二次函数的表达式.(2)、若线段 被 垂直平分,求 的长.(3)、在第一象限的这个二次函数的图象上取一点 ,使得 ,再在这个二次函数的图象上取一点 (不与点 , , 重合),使得 ,求点 的坐标.