江苏省苏州市昆山市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-02 类型:期末考试
一、单选题
-
1. 一元二次方程 中一次项系数、常数项分别是( )A、2, B、0, C、1, D、1,02. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、3. 抽样调查了某年级30名女生所穿鞋子的尺码,数据如下(单位:码)
号码
33
34
35
36
37
人数
7
9
12
1
1
那么这30名女生所穿鞋子的尺码的中位数、众数分别是( )
A、34,35 B、34.5,35 C、35,35 D、35,374. 的直径为 , 点与 点的距离为 ,点 的位置( )A、在⊙O外 B、在⊙O上 C、在⊙O内 D、不能确定5. 在 中, , , ,则 的值为( )A、 B、 C、 D、6. 由二次函数 ,可知( )A、其图象的开口向下 B、其图象的对称轴为直线x=-3 C、其最小值为1 D、当x<3时,y随x的增大而增大7. 如图,圆 为 的外接圆, ,则 的度数为( ) A、15° B、18° C、28° D、30°8. 如图,在半径2的圆形纸片中,剪一个圆心角为90°的扇形(图中阴影部分),则这个扇形的面积为( )
A、15° B、18° C、28° D、30°8. 如图,在半径2的圆形纸片中,剪一个圆心角为90°的扇形(图中阴影部分),则这个扇形的面积为( ) A、π B、 C、2π D、9. 已知二次函数 的图象与 轴交于点 、 ,且 ,与 轴的负半轴相交.则下列关于 、 的大小关系正确的是( )A、 B、 C、 D、10. 如图,在 中, , , , 与 的平分线交于点 ,过点 作 交 于点 ,则 ( )
A、π B、 C、2π D、9. 已知二次函数 的图象与 轴交于点 、 ,且 ,与 轴的负半轴相交.则下列关于 、 的大小关系正确的是( )A、 B、 C、 D、10. 如图,在 中, , , , 与 的平分线交于点 ,过点 作 交 于点 ,则 ( ) A、 B、2 C、 D、3
A、 B、2 C、 D、3二、填空题
-
11. 已知 是方程 的根,则 .12. 要从甲,乙两名运动员中选出一名参加市运会射击项目比赛,对这两名运动员进行了10次射击测试,经过数据分析,甲,乙两名运动员的平均成绩均为8(环),甲的方差为1.2(环2),乙的方差为1(环2),则这10次测试成绩比较稳定的运动员是(填“甲”、“乙”).13. 若关于 的一元二次方程 有实数根,则 的取值范围为.14. 如图,正方形 是一飞镖游戏板,其中点 , , , 分别是各边中点,并将该游戏板划分成如图中所示的9个区域,现随机向正方形内投掷一枚飞镖(投中各区域的边界线或没有投中游戏板,则重投1次),则投中阴影区域的概率是.
 15. 已知一圆锥的母线为 ,底面圆的直径为 ,则此圆锥的侧面积为 (保留 ).16. 如图,已知点 在 轴正半轴上,圆 与 轴相切于原点 ,平行于 轴的直线交圆 于 两点,点 在点 的下方,且点 的坐标是 ,则圆 的半径为.
15. 已知一圆锥的母线为 ,底面圆的直径为 ,则此圆锥的侧面积为 (保留 ).16. 如图,已知点 在 轴正半轴上,圆 与 轴相切于原点 ,平行于 轴的直线交圆 于 两点,点 在点 的下方,且点 的坐标是 ,则圆 的半径为. 17. 已知二次函数 (其中 是自变量),当 时, 随 的增大而增大,且 时, 的最大值为9,则 的值为.18. 如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是.
17. 已知二次函数 (其中 是自变量),当 时, 随 的增大而增大,且 时, 的最大值为9,则 的值为.18. 如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是.
三、解答题
-
19. 计算:20. 解一元二次方程21. 某体育用品商店销售一批运动鞋,零售价每双240元.如果一次购买超过10双,那么每多购1双,所购运动鞋的单价降低6元,但单价不能低于150元,一位顾客购买这种运动鞋付了3600元,这位顾客买了多少双?
22. 一个不透明的袋子中装有四个小球,球面上分别标有数字 ,0,1,2四个数字,这些小球除了数字不同外,其它都完全相同,袋内小球充分搅匀.(1)、随机地从袋中摸出一个小球,则摸出标有数字2的小球的概率为(直接写出答案);(2)、若先从袋中随机摸出一个小球(不放回),然后再从余下的三个小球中随机摸出一个小球.请用树状图或表格形式列出所有可能出现的结果,并求出两次摸出的小球球面上数字之和为1的概率.23. 如图,在四边形 中, , , . .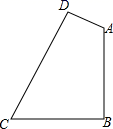 (1)、求 的长;(2)、求四边形 的面积.24. 已知二次函数 ,(1)、若该二次函数的图象与 轴只有一个交点,求此时二次函数的表达式及其顶点坐标;(2)、在平面直角坐标系中,如果该抛物线的顶点到 轴的距离为2,求 的值.25. 如图所示,建筑物 座落在一斜坡的坡顶的平地上,当太阳光线与水平线夹角成60°时,测得建筑物 在坡顶平地上的一部分影子 米,在斜坡 上的另一部分影子 米,且斜坡 的坡度为 (即 ) 求建筑物 的高度.(结果保留根号)
(1)、求 的长;(2)、求四边形 的面积.24. 已知二次函数 ,(1)、若该二次函数的图象与 轴只有一个交点,求此时二次函数的表达式及其顶点坐标;(2)、在平面直角坐标系中,如果该抛物线的顶点到 轴的距离为2,求 的值.25. 如图所示,建筑物 座落在一斜坡的坡顶的平地上,当太阳光线与水平线夹角成60°时,测得建筑物 在坡顶平地上的一部分影子 米,在斜坡 上的另一部分影子 米,且斜坡 的坡度为 (即 ) 求建筑物 的高度.(结果保留根号) 26. 如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为 的中点,连结CE交AB于点F,且BF=BC.
26. 如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为 的中点,连结CE交AB于点F,且BF=BC. (1)、判断直线BC与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为2,sinB= ,求CE的长.27. 如图, 中, , .动点 从点 出发,在 边上以每秒1cm的速度向终点 匀速运动,同时动点 从点 出发,沿 以每秒 的速度向终点 匀速运动,连接 ,设运动时间为 (秒).
(1)、判断直线BC与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为2,sinB= ,求CE的长.27. 如图, 中, , .动点 从点 出发,在 边上以每秒1cm的速度向终点 匀速运动,同时动点 从点 出发,沿 以每秒 的速度向终点 匀速运动,连接 ,设运动时间为 (秒).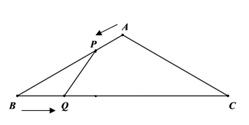
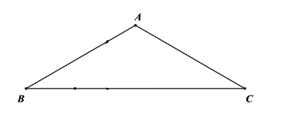 (1)、当 秒时,则 的面积 ;(直接写出答案)(2)、以 为直径作圆 ,在点 , 的运动过程中,当圆 与 的一边所在直线相切时,求 的值.28. 直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 , 两点,与 轴的另一交点为 ,连接 ,点 为 上方的抛物线上一动点.
(1)、当 秒时,则 的面积 ;(直接写出答案)(2)、以 为直径作圆 ,在点 , 的运动过程中,当圆 与 的一边所在直线相切时,求 的值.28. 直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 , 两点,与 轴的另一交点为 ,连接 ,点 为 上方的抛物线上一动点.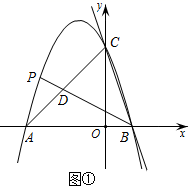
 (1)、求抛物线的解析式;(2)、如图①,连接 ,交线段 于点 ,若 ,求此时点 的坐标;(3)、如图②,连接 .过点 作 轴,交线段 于点 ,若 与 相似,求出点 的横坐标及线段 长.
(1)、求抛物线的解析式;(2)、如图①,连接 ,交线段 于点 ,若 ,求此时点 的坐标;(3)、如图②,连接 .过点 作 轴,交线段 于点 ,若 与 相似,求出点 的横坐标及线段 长.